선형대수와 데이터 사이언스의 관계

실제로 인과 관계를 파악할 수있는 것은 선형적인 것 밖에 없다.
행렬을 최대한 단순하게 표현하는 방법과 이해하는 수학적인 시야들을 공부하는 것이 선형대수이다.
- 선형성: 직선처럼 똑바른 도형, 또는 그와 비슷한 성질을 갖는 대상이라는 뜻이다.

개요

만약 위와 같이 학생들의 시험 점수 데이터를 통해 새로운 기말고사의 점수를 예측한다고 할 때, 회귀 모델을 통해 충분히 풀 수 있다.
하지만 본질적으로 이런 데이터를 파이썬에서 어떻게 표현하고, 저장하고, 계산할 수 있을 지 알아야한다.

데이터 구조(Structure)

1D

데이터의 순서(order)는 유지 되어야 한다.
1차원 데이터를 표현하기 위해서 리스트(list)라는 데이터 구조를 사용한다.

studentA = [89.9, 90.3, 85.1, 87.5]
studentB = [80.1, 84.0, 85.9, 85]

2D

위 데이터를 판다스(Pandas)의 데이터프레임(Dataframe)을 사용해서 더 효율적으로 표현할 수 있다.

import pandas as pd
df = pd.DataFrame([
              [89.9, 90.3, 85.1, 87.5],
              [80.1, 84.0, 85.9, 85]],
              index = ['studentA', 'studentB'], 
              columns = ['mid1', 'mid2', 'mid3', 'final'])
df

이는 리스트안에 리스트를 담는 것과는 또 다른 구조이며, 2차원 리스트, 2차원 어레이(array), 2차원 매트릭스(matrix) 등으로 표현되기도 한다.

매트릭스 계산(Matrix Calculation)

대부분의 데이터는 2차원 이상으로 표현되기 때문에, 이러한 매트릭스 계산을 더 효율적이고 쉽게할 수 있는 방법을 사용할 필요가 있다.

매트릭스 곱(Multiplication)

행렬 계산을 위해선 앞 열의 수와 뒷 행의 수가 같아야 한다.
- $N * M / M * P$

행렬식(Determinant)

2x2

3x3

2차원 매트릭스에 대한 값을 계산 후 수를 곱하여 더한다.

4x4

3차원 매트릭스에 대한 값을 계산 후 수를 곱하여 더한다.

5x5 매트릭스

4차원 매트릭스에 대한 값을 계산 후 수를 곱하여 더한다.
…
…

사용 예제

회귀 모델

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

df = pd.DataFrame([
    [1,3,5,7,9],
    [2,8,14,20,26]],
    index = ['mid','final']
).T

df['ones'] = np.ones(5)
df

X = df[['ones', 'mid']].values
Y = df['final'].values.reshape(-1, 1) # Transpose

# 위의 공식 계산
beta = np.matmul(np.linalg.inv(np.matmul(np.transpose(X), X)), np.matmul(np.transpose(X), Y))

beta
'''
array([[-1.],
       [ 3.]])
'''


Y
'''
array([[ 2],
       [ 8],
       [14],
       [20],
       [26]])
'''


X
'''
array([[1., 1.],
       [1., 3.],
       [1., 5.],
       [1., 7.],
       [1., 9.]])
'''

이를 통해 $Y = X * beta (+ error)$라는 결과에 대입해보면,
- $2 = (1 * -1) + (3 * 1)$
- $8 = (1 * -1) + (3 * 3)$
- …

시각화

# Beta 를 변수로 저장
beta_0 = beta[0, 0]
beta_1 = beta[1, 0]

# 선으로 그림
plt.scatter(df['mid'], df['final'])
axes = plt.gca()
x_vals = np.array(axes.get_xlim())
y_vals = beta_0 + beta_1 * x_vals
plt.plot(x_vals, y_vals, '-', color='b')
plt.title('Grade')
plt.xlabel('Mid')
plt.ylabel('Final')
plt.show()

싸이파이(Scipy) 사용

from scipy import stats
stats.linregress([1, 3, 5, 7, 9], [2, 8, 14, 20, 26])
'''
LinregressResult(slope=3.0, intercept=-1.0, rvalue=1.0, pvalue=1.2004217548761408e-30, stderr=0.0)
'''

PCA, SVD(Dimensionality Reduction)

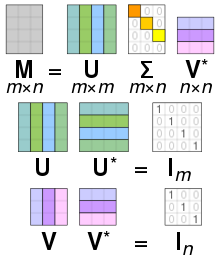
사이즈가 큰 데이터셋을 사이즈가 작은 부분으로 나누는 작업을 할 때 쓰인다.
- 일반적으로 시각화나 다른 모델링을 위해 사용한다.

딥러닝의 CNN

Convolving은 필터, 커널을 통해 이미지를 축소화하여 그 결과물을 분석에 사용하는 방법이다.
필터를 통해서 수정된 이미지는 특수한 부분이 강조되어 이비지 분석에 사용될 수 있다.
이는 선형대수를 기반으로한 단계이다.

import imageio
import matplotlib.pyplot as plt
import numpy as np
import scipy.ndimage as nd
from skimage.exposure import rescale_intensity
from skimage import color

img = imageio.imread('https://i.imgur.com/nItPxZp.png')
plt.axis('off')
plt.imshow(img);

# 이미지를 흑백으로 치환, ( M*N*4 에서 M*N*1로 축소)
grayscale = color.rgb2gray(img)
plt.axis('off')
plt.imshow(grayscale, cmap=plt.cm.gray);

# sobel filter (y axis)
sobel_x = np.array([
    [-1,0,1],
    [-2,0,2],
    [-1,0,1]
])

sobel_x_image = nd.convolve(grayscale, sobel_x)
plt.axis('off')
plt.imshow(sobel_x_image, cmap=plt.cm.gray);

스칼라와 벡터

스칼라와 벡터는 선형대수를 구성하는 기본 단위이다.
스칼라는 단순히 변수로 저장되어 있는 숫자이며, 벡터 혹은 매트릭스에 곱해지는 경우 해당 값에 곱한 값으로 결정된다.
한편 벡터는 파이썬에서는 주로 list로 사용 되며, 이전에 다뤘던 것처럼 데이터셋을 구성하고 있는 데이터프레임의 행/열로써 사용되기도 한다.
매트릭스는 벡터의 모음으로 간주 될 수도 있기 때문에 벡터를 이해하는 것은 매우 중요하다.

스칼라

단일 숫자이며, 변수에 저장 할때는 일반적으로 소문자를 이용하여 표기한다.
스칼라는 실수와 정수 모두 가능하다.

\[a = 5\qquad b = 1.81\qquad c = -3.12\mathrm{e}{+23}\qquad d = \pi\]

import math
import matplotlib.pyplot as plt
import numpy as np

# 시작 벡터 (0,0) 기준
blue = [.5, .3] 

# 스칼라를 곱함
green = np.multiply(5, blue)
red = np.multiply(math.pi, blue)
orange = np.multiply(-3.12, blue)

# 스케일이 바뀐 벡터를 그림
plt.arrow(0, 0, red[0], red[1], head_width = .1, head_length = .1, color = '#d63031')
plt.arrow(0, 0, green[0], green[1], head_width = .1, head_length = .1, color = '#00b894')
plt.arrow(0, 0, blue[0], blue[1], head_width = .1, head_length = .1, color = '#0984e3')
plt.arrow(0, 0, orange[0], orange[1], head_width = .1, head_length = .1, color = '#e17055')
plt.xlim(-2, 3)          
plt.ylim(-2, 2)
plt.title("Vector example 1")
plt.show()

벡터

$n$차원의 벡터는 컴포넌트라 불리는 $n$개의 원소를 가지는 순서를 갖는 모음이다.
(컴포넌트는 스칼라로 간주 되지 않는다.)
벡터는 일반적으로 위의 화살표 (→) 를 갖는 소문자의 형태로 표현된다.
- $\vec{v}$

\[\vec{a} = \begin{bmatrix} 8\\ 9 \end{bmatrix} \qquad \vec{b} = \begin{bmatrix} -4\\ 7\\ 1 \end{bmatrix} \qquad \vec{c} = \begin{bmatrix} 5.5332 \end{bmatrix} \qquad \vec{d} = \begin{bmatrix} Pl\\ x\\ y\\ \frac{2}{3} \end{bmatrix}\]

# 벡터 예시
yellow = [.4, .6]
red = [.11, .12]
blue = [.1, .7]

plt.arrow(0, 0, .4, .6, head_width = .01, head_length = .01, color = '#fdcb6e')
plt.arrow(0, 0, .11, .12, head_width = .01, head_length = .01, color = '#d63031')
plt.arrow(0, 0, .1, .7,  head_width = .01, head_length = .01, color = '#00b894')
plt.title('Vector example 2')
plt.show()

물리학의 관점에서, 벡터는 방향과 크기를 나타낸다.
데이터 사이언스에서, 벡터의 길이(length)는 벡터의 차원수와 동일하다는 정도만 이해하면 된다.

3D Vector

from mpl_toolkits.mplot3d import Axes3D
import numpy as np

# 3번째 요소 추가 
yellow = [.4, .6, .5]
red = [.11, .12, .3]
blue = [.1, .7, .4]

vectors = np.array([[0, 0, 0, .5, .5, .5], 
                    [0, 0, 0, .2, .1, .0],
                    [0, 0, 0, .1, .3, .3]])

X, Y, Z, U, V, W = zip(*vectors) # 몰라도 됩니다. 
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.quiver(X, Y, Z, U, V, W, length=1)
ax.set_xlim([0, 1])
ax.set_ylim([0, 1])
ax.set_zlim([0, 1])
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

벡터의 크기(Magnitude, Norm, Length)

벡터의 Norm 혹은 Magnitude는 단순히 길이에 지나지 않는다.
벡터는 선이기 때문에 피타고라스로 길이를 구할 수 있다.
벡터의 크기를 표현 할때는 ||를 사용한다.

v = [1,2,3,4]
|v| = $\sqrt{ 1^2 + 2^2 + 3^2 + 4^2 }$
|v| = 30
즉, 벡터의 크기는 모든 원소의 제곱을 더한 후 루트를 씌운 값이다.
벡터 크기의 특징은 다음과 같다.

||x||$ \geq 0$
||x||$ = 0$ (모든 원소가 0)
삼각 부등식: ||x + y|| $\leq$ ||x|| + ||y||

백터의 내적(Dot Product)

두 벡터 $\vec{a}$ 와 $\vec{b}$ 의 내적은, 각 구성요소를 곱한 뒤 합한 값이다.

v = [1, 2, 3, 4]
x = [5, 6, 7, 8]
v $\cdot$ x = 1 $\cdot$ 5 + 2 $\cdot$ 6 + 3 $\cdot$ 7 + 4 $\cdot$ 8
= 70
내적은 교환법칙이 적용: $a \cdot b = b \cdot a$
내적은 분배법칙이 적용: $a \cdot (b + c) = a \cdot b + a \cdot c$
벡터의 내적을 위해서는 두 벡터의 길이가 반드시 동일해야 한다.

매트릭스

행과 열을 통해 배치되어있는 숫자들이다.
매트릭스를 표현하는 변수는 일반적으로 대문자를 사용하여 표기한다.

\[X = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} \qquad Y = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \end{bmatrix}\]

판다스를 통해 다뤘던 데이터프레임이 매트릭스와 유사한 형태를 갖는다.

차원(Dimensionality)

매트릭스의 행과 열의 숫자를 차원(dimension, 차원 수 등)이라 표현한다.
차원을 표기 할때는 행을 먼저, 열을 나중에 표기한다.

매트릭스의 일치

2개의 매트릭스가 일치하기 위해서는, 다음 조건을 만족해야 한다.
- 동일한 차원을 보유한다.
- 각 해당하는 구성요소들이 동일하다.

정사각 매트릭스(square matrix)

행과 열의 수가 동일한 매트릭스이다.

\[A = \begin{bmatrix} a_{1,1} \end{bmatrix} \qquad B = \begin{bmatrix} b_{1,1} & b_{1,2} \\ b_{2,1} & b_{2,2} \end{bmatrix} \qquad C = \begin{bmatrix} c_{1,1} & c_{1,2} & c_{1,3} \\ c_{2,1} & c_{2,2} & c_{2,3} \\ c_{3,1} & c_{3,2} & c_{3,3} \end{bmatrix}\]

정사각 매트릭스의 특별한 케이스

대각(Diagonal): 대각선 부분에만 값이 있고, 나머지는 전부 0이다.

\[D = \begin{bmatrix} a_{1,1} & 0 & 0 \\ 0 & a_{2,2} & 0 \\ 0 & 0 & a_{3,3} \end{bmatrix}\]

상삼각(Upper Triangular): 대각선 위쪽 부분에만 값이 있고, 나머지는 전부 0이다.

\[U = \begin{bmatrix} b_{1,1} & b_{1,2} & b_{1,3} \\ 0 & b_{2,2} & b_{2,3} \\ 0 & 0 & b_{3,3} \end{bmatrix}\]

하삼각(Lower Triangular): upper triangular 와 반대로, 대각선 아래에만 값이 있다.

\[L = \begin{bmatrix} c_{1,1} & 0 & 0 \\ c_{2,1} & c_{2,2} & 0 \\ c_{3,1} & c_{3,2} & c_{3,3} \end{bmatrix}\]

단위 매트릭스(Identity):
- Diagonal 매트릭스 중에서, 모든 값이 1인 경우이다.
- 임의의 정사각 매트릭스에 단위 행렬을 곱하면, 그 결과값은 원본 정사각 매트릭스로 나오며,
- 반대로 임의의 매트릭스에 대해서 곱했을때 단위 매트릭스가 나오게 하는 매트릭스를 역행렬 (Inverse)라고 부른다.

\[AI == A, A^{-1}A = I\] \[I_1 = \begin{bmatrix} 1 \end{bmatrix} \qquad I_2 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \qquad I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

대칭(Symmetric): 대각선을 기준으로 위 아래의 값이 대칭인 경우이다.

\[S = \begin{bmatrix} 1 & 2 & 3 \\ 2 & 4 & 5 \\ 3 & 5 & 6 \end{bmatrix}\]

행렬식(Determinant)

행렬식은 모든 정사각 매트릭스가 갖는 속성으로, $det(A)$ 혹은 |A|로 표기된다.
2x2 매트릭스를 기준으로, 행렬식은 다음과 같이(AD-BC) 계산할 수 있다.

\[\qquad \begin{bmatrix} 8 & 12 \\ 9 & 16 \end{bmatrix}\]

$8 * 16 - 12 * 9 = 20$
$/vert x/vert = det(x) = 20$

역행렬(Inverse)

역행렬을 계산하는 방법은 여러가지가 있으며, 행렬의 역수와 같이 표현할 수 있다.
행렬과 그 역행렬의 값은 항상 1(단위 매트릭스)이다.
2x2 매트릭스를 기준으로, 역행렬을 계산하는 방식 중 하나는 아래와 같다.

\[A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \qquad A^{-1} = \frac{1}{ad-bc}\begin{bmatrix} d & -b\\ -c & a \end{bmatrix}\]

매트릭스에 그 역행렬을 곱하면, 단위 매트릭스가 된다.
이것이 중요한 이유는 매트릭스의 곱은 있지만 나눗셈은 선형대수에 존재하지 않기 때문에 대신 그 행렬의 역행렬을 곱한다.

\[𝐴^{−1} 𝐴=𝐼\]

행렬식이 0인 경우

행렬식이 0인 정사각 매트릭스는 ‘특이(singular)’ 매트릭스라고 불린다
이들은 2개의 행 혹은 열이 선형의 관계(M[,i]= M[,j] * N)를 이루고 있을때 발생한다.
매트릭스의 행과 열이 선형의 의존 관계가 있는 경우 매트릭스의 행렬식은 0이다.

\[S = \begin{bmatrix} 10 & 33 & 2 \\ 25 & 66 & 5 \\ 30 & 99 & 6 \end{bmatrix}\]

넘파이(NumPy)

넘파이는 파이썬에서 선형대수를 포함한 많은 종류의 계산에 쓰일 수 있는 라이브러리이다.

2개의 List 더하기

a = [1, 2, 3]
b = [4, 5, 6]

a + b
'''
[1, 2, 3, 4, 5, 6]
'''

2개의 Numpy Array 더하기

import numpy as np

a_np = np.array(a)
b_np = np.array(b)

a_np + b_np
'''
array([5, 7, 9])
'''


a_np * b_np
'''
array([ 4, 10, 18])
'''


a_np - b_np
'''
array([-3, -3, -3])
'''


a_np / b_np
'''
array([0.25, 0.4, 0.5])
'''

리스트와 어레이의 차이는 내용물을 각각 더하는 지의 여부이다.
내적을 계산해볼 것이다.
- 2개의 벡터를 각각 곱하여 더한다.

(a_np * b_np).sum() # a 와 b 벡터의 내적 계산
'''
32
'''


# numpy에 구현되어 있는 함수
np.dot(a_np, b_np)
'''
32
'''


# ndarrays
A = np.array([[1,2], [4,5]])
A
'''
array([[1, 2],
       [4, 5]])
'''


A.T
'''
array([[1, 4],
       [2, 5]])
'''


np.linalg.inv(A)
'''
array([[-1.66666667,  0.66666667],
       [ 1.33333333, -0.33333333]])
'''