베이지안은 여태까지 접했던 통계적 내용과 사뭇 다른 접근을 필요로 한다.
베이지안 방식의 아름다운 점은 내용도 매우 간단하지만, 다양한 분야에 적용이 가능하다는 것이다.

총 확률의 법칙(The Law of Total Probability)

정의에 따르면, $A$라는 특정 확률 변수에 대해 모든 가능한 이벤트의 총 확률은 1이다.

\[P(A) = \sum_n P(A_n) = 1\]

예를 들어 ‘스팸메일이다’라는 ‘확률 변수’는 가능한 이벤트로,
1. 스팸메일인 경우
2. 정상메일인 경우
  - 각각 0.8과 0.2로 총 합은 1이다.
$B$가 일어난 상황에서의, $A$에 대한 확률 $P(A)$는, $P(A \vert B)$의 형태로 표현된다.
(반대로 연관이 없는 경우에는 $B$가 일어난 상황에서, $A$에 대한 확률 $P(A)$는 $P(A)*P(B)$이다.)
예를 들면 ‘스팸메일이다’와 ‘메일 내부에 스팸 단어가 있다’와 같은 이벤트라면,
$P(spam)$ = $P(spam \vert included)P(included)$ + $P(spam \vert not~included)P(not~included)$ 로 표현 할 수 있다.
즉,

\[P(A) = \sum_n P(A \vert B_n)P(B_n)\]

다시 말해, $A$의 모든 확률은, 주어진 $B_n$에 대해, 각각의 일어날 확률의 총합으로 표현될 수 있다.
예를 들어,
$A$ ⇨ 1 or 2
$B$ ⇨ 1 or 2 일 때,
- $p(A=1)$ 일 확률은,
  - $p(B=1) \cdot p( A=1 \vert B=1 )$ 와
  - $p(B=2) \cdot p( A=1 \vert B=2 )$ 인 경우 2가지로 나뉠 것이고,
- $p(A=2)$일 확률은,
  - $p(B=1) * p(A=2 \vert B=1)$ 와
  - $p(B=2) * p(A=2 \vert B=2)$ 인 경우 2가지로 나뉜다.
그렇기 때문에 아래와 같이 표현될 수 있다.

\[p(A=1) = p(B=1) \cdot p( A=1 \vert B=1 ) + p(B=2) \cdot p( A=1 \vert B=2 )\]

조건부 확률(The Law of Conditional Probability)

다른 이벤트가 일어난 상황에서의 조건을 구하기 위해 벤다이어그램을 이용한다.
실제 계산되는 부분의 식은 아래와 같다.

\[P(A \vert B) = \frac{P(A \cap B)}{P(B)}\]

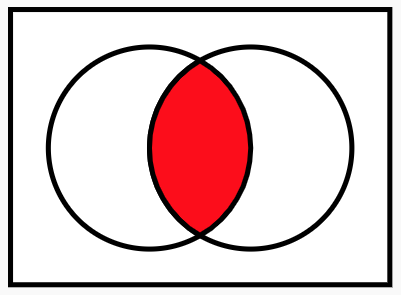
전체 사각형이 모든 가능한 확률 공간이고, $A$는 왼쪽 원, $B$는 오른쪽 원이며, 그 교집합이 가운데 붉은 부분이다.
위 식에 $P(B)$를 양변에 곱하면, $P(A\vert B)P(B) = P(A \cap B)$와 같은 식을 얻을 수 있으며,
이는 곧 $P(A\vert B) = \sum_n P(A \cap B_n)$을 의미한다.
이는, $B$라는 정보가 주어진 상황에서 $A$의 확률은 $B$와 교집합의 합으로 구성되어 있다는 것을 이해할 수 있다.

베이지안 이론(Bayes Theorem)

아래는 베이지안의 핵심 공식과 유도 과정이다.

\[P(A \vert B) = \frac{P(A \cap B)}{P(B)}\] \[P(A \vert B) = \frac{P(B \cap A)}{P(A)}\]

Since

\[P(A \cap B) = P(B \cap A),\]

Therefore

\[P(A \vert B) \cdot P(B) = P(B \vert A) \cdot P(A)\] \[P(A \vert B) = \frac{P(B \vert A)P(A)}{P(B)}\]

이는 $B$가 주어진 상황에서 $A$의 확률은 $A$가 주어진 상황에서의 $B$의 확률 곱하기 $A$의 확률, 나누기 $B$의 확률로 표현된다.
- $p(A \vert B)$ ⇨ 사후 확률(B라는 정보가 업데이트 된 이후의 사(이벤트)후 확률)
- $p(A)$ ⇨ 사전 확률(B라는 정보가 업데이트 되기 전의 사전확률)
- $p(B \vert A)$ ⇨ likelihood
여기서 조건이 붙지 않은 확률은 사전확률(Prior), 조건이 붙은 부분은 사후확률(Updated)로 다시 표현 할 수 있다.

예제

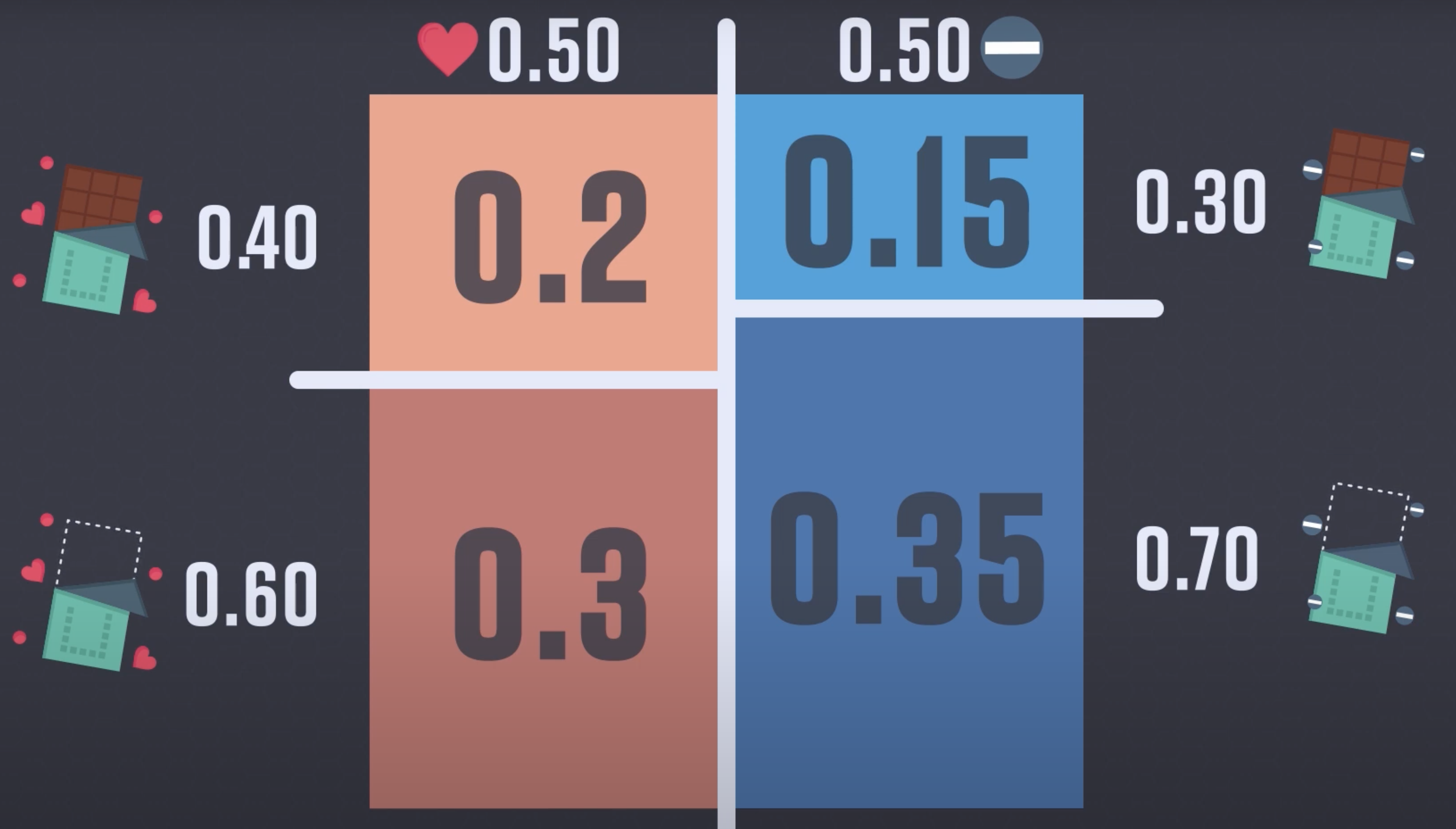
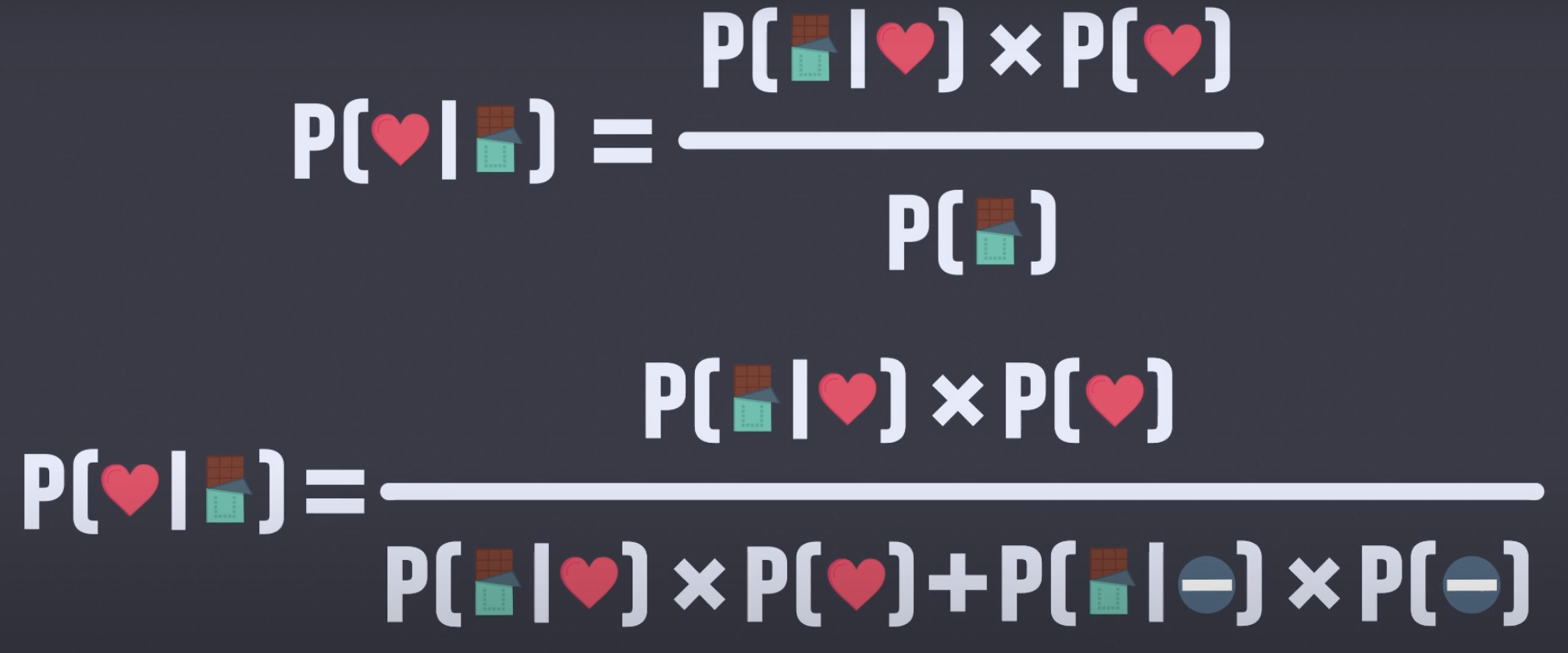
초콜렛을 받았다.
이 사람이 나한테 호감이 있고($p(B)$), 그래서 초콜렛을 줬다($p(A \vert B)$).
이 사람이 나한테 호감은 없고($p(not B)$), 예의상 초콜렛을 줬다($p(A \vert not B)$).

\[p(A) = p(A \vert B) \cdot p(B)+ p(A \vert not B) \cdot p(not B)\]

그림의 예시는 초콜릿을 받았을 때, 그 사람이 나를 좋아할 확률: $p(B∣A)$
$p(B)$ = 좋아할 확률
$p(notB)$ = 안좋아할 확률
$p(A∣B)$ = 좋아하는데 초콜릿을 줄 확률
$p(A∣notB)$ = 안좋아하는데 초콜릿을 줄 확률

\[p(B∣A) = \frac{p(A \vert B) \cdot p(B)}{p(A \vert B) \cdot p(B)+ p(A \vert not B) \cdot p(not B)}\]

베이지안 테스트를 반복하여 사용(repeated testing)

약물을 실제 사용 하는 경우 결과가 양성일 확률은 99%이라고 가정한다.
베이지안을 적용하는 사례는 많지만, 그 중 하나는 약에 대한 양성 반응 테스트이다.
일반적으로, 이 테스트에서 양성 반응이 나온 경우 실제로 약물이 신체에 포함되어 있을 것이라고 생각하지만, 만약 1%의 위양성(FP, False Positive, 실제로 양물이 없지만 양성 반응이 나타남)이 존재하는 경우에도 테스트의 의미는 매우 크게 바뀐다.
실제 분석을 위해, 전체 인구에서 0.5%만이 실제로 약물이 신체에 포함되어 있다고 가정한다.
양성 반은 테스트의 결과가 양성으로 나왔을 경우 실제로 약물이 있을 확률을 베이지안을 통해 검증해볼 것이다.
아래 계산 결과에서 $User$는 실제 약물이 발견 되는 사람, $+$는 양성 반응이다.

$Bayes Theorem Drug Test Example$

즉, 오직 33.2% 정도 만이 양성반응이 나왔다고 해도 실제로 약물을 포함 하는 경우이다.
이러한 이유로 실제 상황에서는 여러번 반복하여 실험한다.
만약 2번을 반복해서 모두 양성이 나오는 경우, 3번을 반복하는 경우…에 따라서 양성 반응이 실제 약물로 부터 나온 결과일 확률이 매우 높아진다.
이처럼 베이지안은 약물의 반응, 음주 측정, 임신 여부와 같이 많은 부분에서 사용되며, 이에 대하여 항상 False Positive와 사전 확률을 통해 정확한 확률을 계산할 수 있어야 한다.

약물 양성 반응 예제

TPR: True Positive Rate(민감도, True Accept Rate) 1인 케이스에 대해 1로 잘 예측한 비율이다(암환자를 암이라고 진단함).
FPR: False Positive Rate(1-특이도, False Accept Rate) 0인 케이스에 대해 1로 잘못 예측한 비율이다(암환자가 아닌데 암이라고 진단함).

# 베이지안 계산을 위해서는 4개의 변수가 필요하다.

p_pos_used = 0.99 # True positive rate (TPR, Sensitivity)
p_used = 0.005 # prior probability
p_pos_not_used = 0.01 # False positive rate (FPR)
p_not_used = 1 - p_used # 1 - p_used  

numerator = p_pos_used * p_used 

denominator = (p_pos_used * p_used) + (p_pos_not_used * p_not_used)

posterior_probability = numerator / denominator

posterior_probability
'''
0.33221476510067116
'''


p_pos_used = 0.99 # TPR
p_used = 0.332 # prior probability
p_pos_not_used = 0.01 # FPR
p_not_used = 1 - p_used # 1 - p_used  

numerator = p_pos_used * p_used 

denominator = (p_pos_used * p_used) + (p_pos_not_used * p_not_used)

posterior_probability = numerator / denominator

posterior_probability
'''
0.980081106870229
'''


p_pos_used = 0.99 # TPR 
p_used = 0.98008 # prior probability
p_pos_not_used = 0.01 # FPR
p_not_used = 1 - p_used # 1 - p_used  

numerator = p_pos_used * p_used 

denominator = (p_pos_used * p_used) + (p_pos_not_used * p_not_used)

posterior_probability = numerator / denominator

posterior_probability
'''
0.9997947404084419
'''

몬티홀의 베이지안

가정

처음에 1번 문을 선택한다.
- $H$(Hypothesis): 1번 문 뒤에 자동차가 있다.
- $E$(Evidence): 진행자가 염소가 있는 문을 1개 열어준다.

베이지안

\[P(A\vert B) = \frac{P(B\vert A)P(A)}{P(B)}\]

목적은 진행자가 문을 보여준 상태$P(E)$에서 선택했던 문에 자동차가 있을 확률 $P(H)$ ⇨ $P(H\vert E)$

\[P(H\vert E) = \frac{P(E\vert H)P(H)}{P(E)} = \frac{P(E\vert H)P(H)}{P(E\vert H)P(H)+P(E\vert not H)P( not H)}\]

구해야 하는 것

$P(E\vert H)$
- $P(E\vert H)$ = 1번 문에 자동차가 있는 상황에서 진행자가 염소가 있는 문을 1개 열어줄 확률 = 1
$P(H)$
- $P(H)$ = 자동차가 1번문에 있을 확률 : $\frac{1}{3}$
$P(E\vert not H)$
- 마찬가지로 $P(E\vert not H)$ = 1
$P(not H)$
- $P(not H)$ = $\frac{2}{3}$

계산

\[P(H\vert E) = \frac{1 \cdot \frac{1}{3}}{1 \cdot \frac{1}{3} + 1 \cdot \frac{2}{3}} = \frac{\frac{1}{3}}{1} = \frac{1}{3}\]

염소가 있는 다른 문이라는 추가 정보($E$)가 있는 상황에서 처음에 선택했던 1번 문에 자동차가 있을 확률($H$)은 $\frac{1}{3}$ 으로 계산된다.

동전 던지기의 베이지안

처음 가정을 동전을 던졌을 때 앞면이 나올 확률이 0부터 1까지 고르게 분포되어 있다고 잡는다.
동전을 여러번 던지면서 해당 정보를 반영하고, 이를 통해 동전을 던졌을 때 앞면이 나올 확률을 점점 추정해본다.

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
from IPython.core.pylabtools import figsize

figsize(15, 9)

dist = stats.beta
n_trials = [0, 1, 2, 3, 4, 5, 8, 15, 50, 300, 500, 1000]
data = stats.bernoulli.rvs(0.5, size = n_trials[-1]) # binomial with p(h) = 0.5
x = np.linspace(0, 1, 100)

for k, N in enumerate(n_trials):
  sx = plt.subplot(len(n_trials) / 2, 2, k+1)
  plt.xlabel("P(H)", fontsize = 13) if k in [0, len(n_trials) - 1] else None
  plt.setp(sx.get_yticklabels(), visible = False)
  heads = data[:N].sum()
  y = dist.pdf(x, 1 + heads, 1 + N - heads)
  plt.plot(x, y, label = 'Trial %d \n Head %d Times' % (N, heads))
  plt.fill_between(x, 0, y, color = '#348abd', alpha = .4)
  plt.vlines(0.5, 0, 4, color = 'k', linestyles = '--', lw = 1)

  leg = plt.legend()
  leg.get_frame().set_alpha(0.4)
  plt.autoscale(tight = True)

plt.suptitle('Bayesian Update (Probability of Head)', y = 1.02, fontsize = 14)
plt.tight_layout()

신뢰구간의 베이지안

import numpy as np

from scipy import stats

coinflips = np.random.binomial(1, 0.5, 20)
coinflips
'''
array([1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0])
'''

프리퀀시 기반 신뢰구간 추정

def confidence_interval(data, confidence = 0.95):
  
    """
      주어진 데이터의 표본 평균에 대한 신뢰 구간을 계산
      기본 값으로 t-분포와 양방향(two-tailed), 95%의 신뢰도를 사용
  
      입력 값 : 
        data - 여러 개로 이루어진 (list 혹은 numpy 배열) 표본 관측치
        confidence - 신뢰구간을 위한 신뢰도 
      
      반환 되는 값:
        (평균, 하한, 상한구간)으로 이루어진 tuple
    """
  
    data = np.array(data)
    mean = np.mean(data)
    n = len(data)
    s = data.std(ddof = 1)
    stderr = s / np.sqrt(n)
    print(stderr)
    
    t = stats.t.ppf( (1 + confidence) / 2.0 , n - 1)
    margin_of_error = t * stderr
    interval = stderr * stats.t.ppf((1 + confidence) / 2.0, n - 1)
    return (mean, mean - interval, mean + interval)

confidence_interval(coinflips)
'''
0.1094243309804831
(0.35, 0.12097224312031754, 0.5790277568796824)
'''

베이지안 기반 신뢰구간 추정(SciPy)

# https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.bayes_mvs.html#scipy.stats.bayes_mvs

mean_CI, _, _ = stats.bayes_mvs(coinflips, alpha = .95) # mean , variance, std

# mean_cntr, var_cntr, std_cntr

mean_CI
'''
Mean(statistic=0.35, minmax=(0.12097224312031751, 0.5790277568796824))
'''
# 윗 결과와 유사함

옵티마이즈(Optimize)

!pip3 install bayesian-optimization


def black_box_func(x, y):
  return -x ** 2 - (y-1) ** 2 + 1

pbounds = {'x' : (2, 4), 'y': (-3, 3)}

from bayes_opt import BayesianOptimization

optimizer = BayesianOptimization(f = black_box_func, 
                                 pbounds = pbounds, 
                                 random_state = 1)

optimizer.maximize(init_points = 2, n_iter = 10) 
'''
|   iter    |  target   |     x     |     y     |
-------------------------------------------------
|  1        | -7.135    |  2.834    |  1.322    |
|  2        | -7.78     |  2.0      | -1.186    |
|  3        | -7.11     |  2.218    | -0.7867   |
|  4        | -11.09    |  3.288    | -0.1305   |
|  5        | -4.335    |  2.299    |  0.7729   |
|  6        | -4.023    |  2.172    |  1.552    |
|  7        | -3.605    |  2.137    |  1.195    |
|  8        | -3.004    |  2.0      |  0.9407   |
|  9        | -3.122    |  2.0      |  0.6503   |
|  10       | -4.426    |  2.0      |  2.194    |
|  11       | -3.085    |  2.0      |  1.292    |
|  12       | -31.0     |  4.0      | -3.0      |
=================================================
'''


print(optimizer.max)
'''
{'target': -3.0035155160504425, 'params': {'x': 2.0, 'y': 0.9407082126223019}}
'''


import numpy as np

res = -9999
x_val = -9999
y_val = -9999

iter_cnt = 0

for x in np.arange(2, 40.1, 0.1):
  for y in np.arange(-3, 30.1, 0.1):
    curr_res = black_box_func(x, y)
    iter_cnt += 1

    if curr_res > res:
      res = curr_res
      x_val = x
      y_val = y

print(iter_cnt)
print(res)
print(x_val)
print(y_val)
'''
126111
-3.0
2.0
1.0000000000000036
'''

전범위 조사 결과
- $x$ = 2, $y$ = 1~ 일때가 Maximized value
Bayesian
- $x$ = 2, $y$ = 0.9407 일때가 Maximized value

[통계] 베이지안 통계 개론(Bayesian Inference)