아노바(ANOVA)

2개 이상 그룹의 평균에 차이가 있는지를 가설 검정하는 방법이다.

다중 비교 문제(Multiple Comparision)

2개 이상의 그룹을 비교할 때 각각 두 개 씩 여러번 T-Test를 하게 되면 에러가 날 확률이 커진다.

만약 m개 그룹에 대한 가설 검정이라면, $\bar{\alpha} = {1 - (1 - \alpha)}^{m}$ , $\bar{\alpha} \leq m \cdot {\alpha}$ 라는 것이 수학적으로 증명되어 있다.

여러 개를 하나하나 비교하는 것은 그룹 수가 늘어날 수록 에러도 커지기 때문에 한꺼번에 비교하는 방법이 필요하다.

변화(Variation)

여러 그룹 간 차이가 있는 지 확인하기 위해선 여러 그룹들이 하나의 분포에서 왔다라는 가정이 나오게 된다.
이를 위한 지표는 F-statistic이며 식은 아래와 같다.

\[F = { {Variance-between-group} \over {Variance-with-in-group} }\]

위 F값이 높다는 것이 의미하는 바는,
- 분자(다른 그룹끼리는 분산)는 크고, 분모(전체 그룹의 분산)은 작아야 한다.
- 즉, 다른 그룹끼리의 분포가 다를것이다. 라는 가정이 붙는다.

공식 및 계산

$m$ = 전체 그룹 수, $n$ = 데이터 수

\[S_{w} = \sum_{i = 1}^{m} \sum_{j=1}^{n} (x_{ij} - x_{i.})^2\] \[x_{i.} = \sum_{j = 1}^{n} {x_{ij} / n}\] \[S_{b} = n \sum_{i=1}^m (x_{i.} - x_{..})^2\] \[x_{..} = {{\sum_{i=1}^m x_{i.} } \over {m}}\] \[F = { { S_{b}}/{(m-1)} \over S_{w} / (nm-m)}\] \[p( {F_{m-1, nm-m}} > F_{m-1, nm-m, \alpha}) = \alpha\]

싸이파이(Scipy) 이용 구현

import numpy as np

g1 = np.array([0, 31, 6, 26, 40])
g2 = np.array([24, 15, 12, 22, 5])
g3 = np.array([32, 52, 30, 18, 36])

from scipy.stats import f_oneway

f_oneway(g1, g2, g3) # pvalue = 0.11 

많은 샘플(Many Samples)

큰 수의 법칙(Law of large numbers)

샘플의 데이터의 수가 커질 수록, 샘플의 통계치는 점점 모집단의 모수와 같아진다.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

population = np.random.normal(50, 10, 1000) # mu = 50, sd = 1, 
population.var() # 94.67645805499781

np.random.choice(population, 5).var() # 46.4

np.random.choice(population, 15).var() # 106.1

np.random.choice(population, 50).var() # 107.8

np.random.choice(population, 100).var() # 103.0

np.random.choice(population, 200).var() # 104.0


dat = []

for i in np.arange(start = 5, stop = 995, step = 5) :
  s = np.random.choice(population, i)
  dat.append(s.var())
dat

(pd
 .DataFrame(dat)
 .plot
 .line(color = '#4000c7')
 .axhline(y = 100, color = '#00da75')
 );

사건을 무한히 반복할 때 일정한 사건이 일어나는 비율은 횟수를 거듭하면 할수록 일정한 값에 가까워진다.

중심 극한 정리(Central Limit Theorem, CLT)

샘플의 데이터의 수가 많아질 수록, 샘플의 평균은 정규분포에 근사한 형태로 나타난다.

sample_means1 = []
for x in range(50):
  coinflips = cdf['초미세먼지(㎍/㎥)'].sample(x)
  sample_means1.append(coinflips.mean())
  
sample_means2 = []
for x in range(200):
  coinflips = cdf['초미세먼지(㎍/㎥)'].sample(x)
  sample_means2.append(coinflips.mean())
  
sample_means3 = []
for x in range(700):
  coinflips = cdf['초미세먼지(㎍/㎥)'].sample(x)
  sample_means3.append(coinflips.mean())

sns.histplot(sample_means1, color = '#e74c3c');
plt.show()

sns.histplot(sample_means2, color = '#f39c12');
plt.show()

sns.histplot(sample_means3, color = '#27ae60');
plt.show()

모집단의 분포에 상관없이 임의의 분포에서 추출된 표본들의 평균의 분포는 정규 분포를 이룬다.
중심 극한 정리로 인해 다음 두 가지가 가능해진다.
- 샘플 수가 30개 이상이라면, 모집단의 평균과 분산을 알아낼 수 있다.
- 모든 샘플들은 정규 분포로 나타낼 수 있으며, 정규 분포와 관련된 수학적 이론을 적용할 수 있게 된다.

신뢰도

통계에서 어떠한 값이 알맞은 모평균이라고 믿을 수 있는 정도이다.
즉, 신뢰도가 95% 라는 의미는 표본을 100번 뽑았을때 95번은 신뢰구간 내에 모집단의 평균이 포함된다.

신뢰구간의 설정 및 해석

신뢰구간 포스팅 바로가기

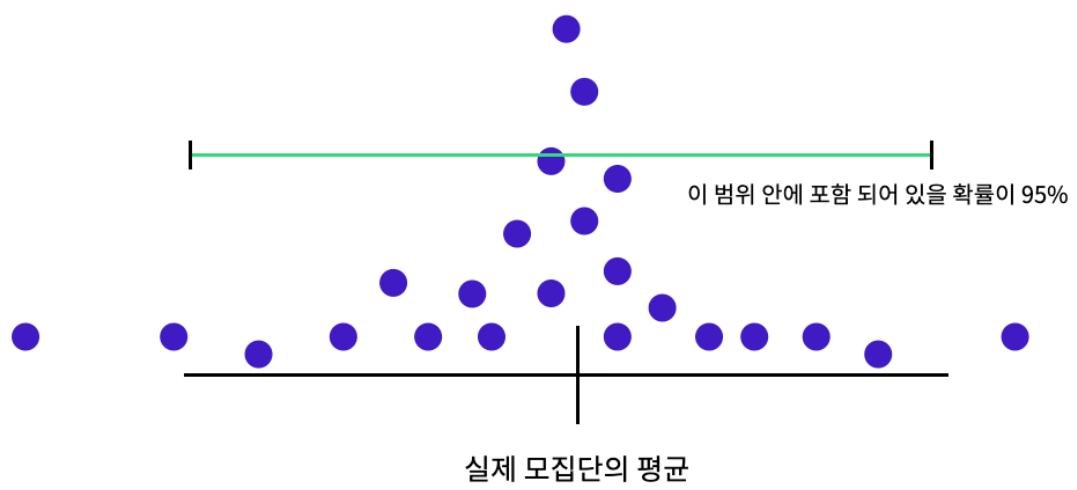
위 그림의 구간을 수학적으로 표현한 내용은 아래의 식과 같다.

\[\bar {x} \pm {t \cdot {s \over \sqrt{n}}}\]

$\bar{x}$는 estimated mean, $ {t \cdot {s \over \sqrt{n} } }$는 error라고 부른다.

싸이파이(scipy)에서의 신뢰 구간

np.random.seed(123)

data2 = np.random.normal(50, 10, 1000)

sample = np.random.choice(data2, 10)

confidence_interval(sample)
'''
(44.28501220284126, 37.93312500671013, 50.63689939897239)
'''


from scipy.stats import t

# 표본의 크기
n = len(sample)
# 자유도
dof = n-1
# 표본의 평균
mean = np.mean(sample)
# 표본의 표준편차
sample_std = np.std(sample, ddof = 1)
# 표준 오차
std_err = sample_std / n ** 0.5 # sample_std / sqrt(n)

CI = t.interval(.95, dof, loc = mean, scale = std_err)
print("95% 신뢰구간: ", CI)
'''
95% 신뢰구간:  (37.93312500671013, 50.63689939897239)
'''

신뢰 구간 시각화

x = np.linspace(0, 100, 101) # 0 ~ 100 by 100 
y = stats.norm(50, 10).pdf(x) 

# plt.plot([A, A], [B, C]) : (A, B) ~ (A,C) 까지의 Line
plt.plot(x, y) # blue line

plt.plot([50, 50], [0, 0.05], 'k-', lw = 2, color = '#ff6f15') 

# 30 sample
plt.plot([53.54,53.54], [0, 0.05], 'k:', lw = 2, color = '#4000c7')
plt.plot([46.46,46.46], [0, 0.05], 'k:', lw = 2, color = '#4000c7');

# 10 sample
plt.plot([56.35,56.35], [0, 0.05], 'k--', lw = 2, color = '#e84118')
plt.plot([43.65,43.65], [0, 0.05], 'k--', lw = 2, color = '#e84118');

# 3 sample

plt.plot([82.72,82.72], [0, 0.05], 'k-', lw = 2, color = '#44bd32')
plt.plot([17.29,17.29], [0, 0.05], 'k-', lw = 2, color = '#44bd32');

[통계] 아노바와 CLT 그리고 신뢰 구간(CI)이란?