[통계] 가설 검정(Hypothesis Test)이란?

• 통계는 데이터를 다루는 목적에 따라 크게 두 가지로 구분할 수 있다.
  • 하나는 기술 통계(Descriptive Statistics) 그리고 다른 하나는 추리 통계(Inferential Statistics)이다.
• 기술 통계란 수집한 데이터를 요약 묘사 설명하는 통계 기법이다.
• 기술 통계에는 크게 두 가지로 구분할 수 있다.
  • 하나는 우리가 수집한 데이터를 대표하는 값이 무엇인지 또는 어떤 값에 집중되어 있는 지를 다루는 기법이다.
    • 데이터의 집중화 경향(Central tendency)에 대한 기법이라 말할 수 있다.
    • 평균, 중앙값, 최빈값 등이 바로 집중화 경향에 속하는 것들이다.
  • 또 다른 하나는 우리가 수집한 데이터가 어떻게 퍼져 있는 지 설명하는 기법이다.
    • 이를 분산도(Variation)라고 부른다.
    • 분산도는 말 그대로 데이터가 전반적으로 어떻게 분포되어 있는 지 즉, 뭉쳐 있는 지 퍼져 있는 지를 설명하는 방법이다.
    • 대표적으로 표준편차, 사분의 값 등이 있다.

기술 통계치(Descriptive Statistics)란?

• 수집한 데이터를 count, mean, standard dev, min, 1Q, median, 3Q, max 등으로 설명 하는 값(혹은 통계치)이다.

• 기술 통계 기법을 통해 수집한 데이터의 전체적인 모양을 그릴 수 있다.
• 우리나라의 국민 1인당 평균 소득이 2만 달러라고 가정하면, 이 값은 우리나라 국민의 소득 수준의 대표값이다.
• 하지만 대표값 뿐 아니라 분산도 중요하다.
• 국민 1인당 평균 소득이 아무리 높아도, 소득에 대한 편차도 함께 높은 값을 지니고 있다고 가정하면, 소득 분포가 넓게 분포되어 있다는 뜻이고, 이는 다시 말해 국민의 소득 편차가 크다는 뜻이다.
• 이를 통해 소득의 분배가 잘 이루어지지 않음을 해석할 수 있다.

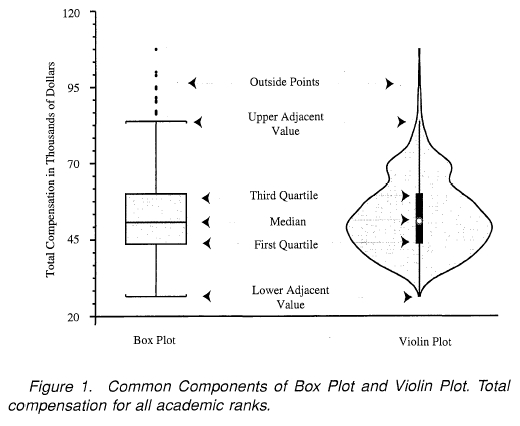
기술 통계치의 시각화

Box plot

Bag plot

Violin plot

추리 통계치(Inferetial Statistics)란?

• 수집한 데이터를 바탕으로 추론 예측하는 통계 기법이다.
• 말 그대로 수집한 데이터를 기반으로 어떠한 것을 추론하고 예측하는데 사용하는 통계 기법을 말한다.
• 대표적인 추리 통계의 예로 대통령 선거 예측을 들 수 있다.

• 미국 대선에서 모두 힐러리가 당선될 것이라고 예측 했는데, 설문 조사를 통한 것이었다.
• 물론 예측은 맞지 않았고, 이 사건은 추리 통계라는 것이 결국 확률을 말할 뿐이지 노스트라다무스처럼 예언을 하는 것이 아니라는 것을 다시금 일깨워주었다.
• 왜냐하면 제한된 데이터 즉, 표본을 사용하기 때문이다.
• 결국 이로써 빅데이터의 중요성이 더욱 강조 되었고, 어쨌든 추리 통계는 그 결과가 다 맞는 것이 아닐지라도 굉장히 중요한 통계 기법이다.

• Population
• Parameter
• Statistic
• Estimator
• Standard Deviation
• Standard Error

Effective Sampling

• 샘플링 기법에는 여러가지 방법이 있다.

1. Simple Random Sampling

• 모집단에서 무작위로 샘플링하는 방법이다.

2. Systematic sampling

• 모집단에서 샘플링을 할 때 규칙을 가지고 추출하는 방법이다.
  • ex) 1, 6, 11, 16, … 번째의 데이터를 선택

3. Stratified random sampling

• 모집단을 미리 여러 그룹으로 나누고, 그 그룹별로 무작위 추출을 수행하는 방법이다.
  • ex) 여론 조사를 위해 사람을 나이대 별로 나누고, 해당 그룹안에서 무작위 추출

4. Cluster sampling

• 모집단을 미리 여러 그룹으로 나누고, 이후 특정 그룹을 무작위로 선택하는 방법이다.

기술 통계 vs 추리 통계

• 둘 다 중요하지만 개인적으로 추리 통계가 더 중요하다고 생각한다.
• 통계를 사용하는 중요한 목적은 바로 우리가 모르지만 알고 싶어하는 것을 예측하고 설명하는 것이기 때문이다.
• 이러한 것을 우리는 추리 통계를 이용해서 확률적으로 추론할 수 있다.

가설 검정(hypothesis test)이란?

• 통계적 추론의 하나로서, 모집단 실제의 값이 얼마가 된다는 주장과 관련해, 표본의 정보를 사용해서 가설의 합당성 여부를 판단하는 과정이다.
• 주어진 상황에 대해서, 하고자 하는 주장이 맞는지 아닌지를 판정하는 과정이다.
• 모집단의 실제 값에 대한 sample의 통계치를 사용해서 통계적으로 유의한지 아닌지 여부를 판정한다.

우연성에 따른 결과

1 2 3 4 5

np.random.seed(1111) df = pd.DataFrame({'coinflips': np.random.binomial(n = 1, p = 0.5, size = 10)}) df.hist();

• 무작위성을 고려하더라도 샘플의 사이즈가 클수록 더 높은 신뢰성을 보이는 걸 알 수 있다.

1 2	pd.DataFrame(np.random.binomial(n = 1, p = 0.5, size = 100)).hist(); pd.DataFrame(np.random.binomial(n = 1, p = 0.5, size = 1000)).hist();

표본 평균의 표준 오차( Standard Error of the Sample Mean )

• $S$ (우측) = 표본의 표준편차 (sample standard deviation)
• $N$ = 표본의 수 (sample size)
  • 결론: 표본의 수가 더욱 많아질수록, 추측은 더 정확해지고(평균) 높은 신뢰도를 바탕으로 모집단에 대해 예측 할 수 있도록 한다.

Student T-test

One Sample t-test

• 1개의 sample 값들의 평균이 특정값과 동일한지 비교한다.

• 동전이 공정한지 확인하려고 할 때: $p(x = H) = 0.5$
• 모집단에 대한 정보와 표본의 데이터를 비교한다.

• 위 통계치는 평균을 빼고 표준편차로 나눠줬는데 이러한 과정을 정규화라고 하며, 이 과정을 하게 되면 주어진 데이터가 평균은 0, 표준 편차가 1인 데이터로 스케일링된다.

T-test Process

1. 귀무 가설을 설정(보통 상관관계가 없다고 설정한다.)

• 귀무가설: 모집단의 특성에 대해 옳다고 제안하는 잠정적인 주장이다.
  • $H_0: \mu = \bar{x}$
  • $\mu$ = 모집단의 평균
  • $\bar{x}$ = 표본의 평균

2. 대안 가설 설정

• 대안가설: 귀무가설이 거짓이라면 대안적으로 참이 되는 가설이다.
  • $H_1: \mu \neq \bar{x}$

3. 신뢰도 설정(보통 95%)

• 신뢰도(Confidence Level): 모수가 신뢰 구간 안에 포함될 확률이다.(보통 95, 99% 등을 사용한다.)
  • 신뢰도 95% = 모수가 신뢰 구간 안에 포함될 확률이 95% = 귀무 가설이 틀렸지만 우연히 성립할 확률이 5%

4. P-value 확인

• 주어진 가설에 대해 얼마나 근거가 있는 지에 대한 값을 0과 1사이의 값으로 스케일링한 지표로서, P-value가 낮다는 것은, 귀무 가설이 틀렸을 확률이 높다는 것이다.
  • ex) P-value가 0.05다.
    => 우리가 뽑은 샘플 데이터로 낼 수 있는 결론이 귀무 가설이 (틀렸지만 우연히 맞을 ) 확률이 0.05다. => 귀무가설은 틀렸다

5. 가설에 대한 결론

P-value의 기준

• P-value : 유의 확률, 귀무가설이 맞다고 가정할 때 얻은 결과보다 극단적인 결과가 실제로 관측될 확률

1. pvalue < 0.01
   • 귀무 가설이 옳을 확률이 1% 이하이다. => 틀렸다.(깐깐한 기준)
2. pvalue < 0.05 (5%)
   • 귀무 가설이 옳을 확률이 5%이하이다. => 틀렸다.(일반적인 기준)
3. 0.05 < pvalue < 0.1(애매하다.)
   • 실험을 다시 한다.
   • 데이터를 다시 뽑는다.
   • 샘플링을 다시 한다.
   • 기존의 경험,인사이트를 바탕으로 가설에 대한 결론을 내린다.
4. pvalue > 0.1 (10%)
   • 귀무 가설이 옳을 확률이 10% 이상 인데, => 귀무가설이 맞다. ~ 틀리지 않았을 것이다.
   • ex) p-value: 0.85 => 귀무 가설은 틀리지 않았다.(귀무가설이 옳다와 톤이 약간 다르다.)

One-side test vs Two-side test

• Two side (tail/direction) test
  • 샘플 데이터의 평균이 ‘“X”와 같다./같지 않다.’를 검정하는 내용이다.
• One side test
  • 샘플 데이터의 평균이 ‘“X”보다 크다. 혹은 작다./크지 않다. 작지 않다.’를 검정하는 내용이다.

Two sample T-test

• 2개의 샘플 값들의 평균이 서로 동일한 지 비교한다.

1. 귀무가설: 두 확률은 같다.(차이가 없다.)
   • $H_0: \bar{x}_1 = \bar{x}_2$
2. 대안가설: 같지 않다.
   • $H_1: \bar{x}_1 \neq \bar{x}_2$
3. 신뢰도: 95%

참조

• 기술 통계와 추리 통계란 무엇인가?
• 통계적 가설 검정