[통계] 데이터 사이언스에서의 미분 기초

Posted on | In
최적화와 미분의 관계, 미분 / 편미분 / Chain Rule의 차이를 이해, 파이썬을 이용한 도함수 구현

미분

  • 작을 미(微)와 나눌 분(分). ‘함수를 작게 나눈다’라는 의미이다.
  • x의 값을 아주 아주 미세하게 변화 시킨 후에 입력했을 때 (예를 들면 0.00000000000000000001 혹은 더 0에 최대한 가깝게) 그 결과값이 어떻게 바뀌는지를 보는 것이 미분이다.
  • 아래의 그림처럼 $\Delta x$를 점점 0 에 가깝게해서, 순간의 변화량을 측정하고자 하는것이 더 구체적인 목표다.

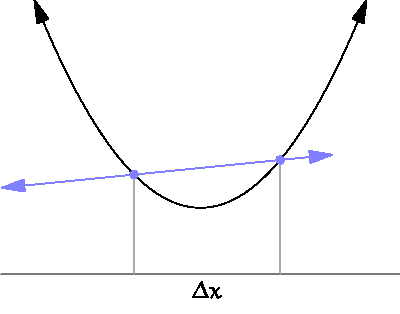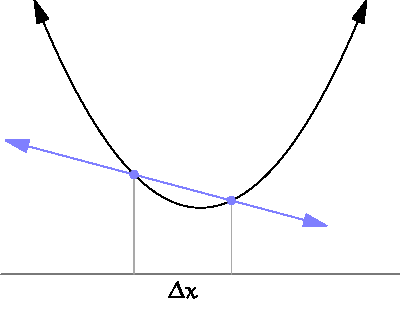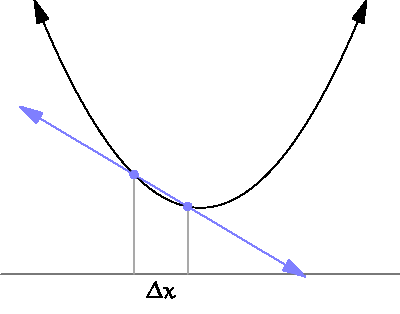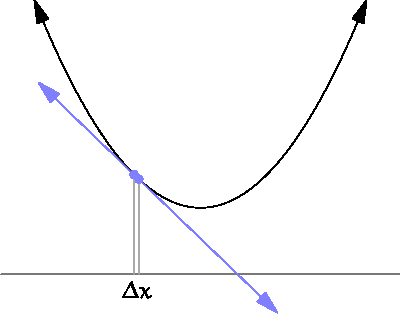
  • 특정한 파라미터 값(input, x)에 대해서 나오는 결과값(output, y)이 변화하는 정도를 (0에 가까운 부분을 찾기 위해) 계산하는 것으로 이해하면 된다.

미분과 데이터 사이언스의 상관 관계

  • 아래와 같은 데이터 분포가 있다고 가정한다.
1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 랜덤하게 평균 0, 표준편차 1의 가우시안 표준 정규 분포 난수 x, y를 50개씩 뽑는다.
np.random.seed(42)
x = np.random.randn(50)
y = np.random.randn(50)

# 산점도를 통해 x,y를 시각화
sns.regplot(x, y)
plt.show()

  • x를 넣었을 때, y 값을 예측하는 선형 모델은 아래와 같이 나타낼 수 있다.
    • $ \hat y = a + b X $
    • 여기서 $\alpha$는 y-절편(y-intercept), $\beta$는 기울기(slope)이다.
  • 주어진 데이터 X를 넣었을 때 모델이 예측하는 예측값과 실제값 간의 차이(Error, $\varepsilon$)를 계산한 다음, 여러 모델 중 Error(모델에서 예측하는 예측값과 실제값(y)의 차이)가 가장 작은 모델을 선택하는 방법을 통해, 가장 좋은 모델을 선택 할 수 있다.
  • 이 과정은 $f(a,b) = \varepsilon$ 로 표현, 오차 함수인 $\varepsilon$을 최소화 하는 $a,b$를 찾는 것이 머신러닝(Linear regression)의 목표이다.
  • 선형회귀모델의 경우 오차 함수는 보통 MSE(Mean Squared Error)를 사용한다.
  • 오차 함수를 최소화하는 $a,b$를 구하기 위해서 미분을 사용한다.
  • 미분을 통해서 오차 함수의 도함수($f’(x)$)가 0이 되는 부분(즉, 변화율이 0인 부분)을 찾아서 오차 함수가 최소화되는 $a,b$을 찾는 것이다..

미분 공식 w/ Python

기본 미분 공식

  1. $f’(x) = {f(x + \Delta x) - f(x) \over \Delta x}$, $\Delta x \rightarrow 0$
    실제로 0으로 나눌 수는 없기 때문에 0에 매우 근사한 값을 사용한다.
    보통 $1e-5$를 사용하며, 이러한 접근 방식을 numerical method 라는 방법으로 표현한다.
  2. $f(x + \Delta x) - f(x - \Delta x) \over 2\Delta x$

머신러닝 미분 공식

1. $f(x)$ = 상수 $\rightarrow$ $f’(x)$ = 0

  • f’(x)가 상수(constant)인 경우에는 x를 아무리 늘리거나 줄여도 늘 같은 숫자이기 때문에 변화가 전혀 없다.
  • 그 말은 즉 변화율이 0이기 때문에 미분계수도 늘 0이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 예시 1 : Numerical Method

# f(x) = 5
def f(x):
    return 5

def numerical_derivative(fx, x):
    delta_x = 1e-5

    return (fx(x + delta_x) - fx(x)) / delta_x

print(numerical_derivative(f, 1))

# 예시 2 : Scipy의 derivative 활용
from scipy.misc import derivative

# 두 방법의 결과값 비교
derivative(f,1, dx=1e-6) == numerical_derivative(f, 1)

'''
0.0
True
'''

2. Power Rule : $f(x) = ax^{n}$ $\rightarrow$ $f’(x) = an{x}^{(n-1)}$

  • ex) $f(x) = 3x^4 + 10$
  • 먼저 4승에서 하나를 내려보내서 앞에 있는 3과 곱해준다.(10은 상수이기 때문에 미분을 하면 0이다.)
    $f’(x) = (4*3)x^4$
  • 이후에는 4승에서 1을 빼준다.(빌려줬기 때문에)
    $f’(x) = (4*3)x^{4-1}$
  • 최종적으로 f(x)의 도함수는 이렇게 계산된다.
    $f’(x) = 12x^3$
  • x = 2일 때
    $f’(2) = 96$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 같은 결과를 numerical method를 활용해서 계산
def f(x):
    return 3*(x**4) + 10

def numerical_derivative(fx, x):
    delta_x = 1e-5

    return (fx(x + delta_x) - fx(x)) / delta_x

print(numerical_derivative(f, 2))

# 예시 2 : Scipy의 derivative 활용
from scipy.misc import derivative

# 두 방법의 결과값 비교
print(derivative(f,2, dx=1e-5))
derivative(f,2, dx=1e-5) == numerical_derivative(f, 2)  #delta X의 값은 같지만 Rounding 에러로 인해 두 결과가 미묘하게 다른 것을 확인하실 수 있습니다.

'''
96.0007200028201
96.0000000031158
False
'''

3. $f(x) = e^x$ $\rightarrow$ $f’(x) = e^x$

  • 도함수 역시 지수 함수이다.

4. $f(x) = lnx$ $\rightarrow$ $f’(x) = {1 \over x}$

  • 자연 로그의 미분은 Logistic Regression이나 신경망의 활성 함수인 sigmoid 함수를 미분할 때 상당히 편하게 미분을 할 수 있도록 도와준다.
  • sigmoid 함수에 자연로그를 씌움으로서 미분을 훨씬 수월하게 할 수 있게 되기 때문이다.

편미분

  • 머신러닝의 Error 함수는 여러개의 파라미터 값을 통해 결정된다.
  • 파라미터가 2개 이상인 Error 함수에서 ‘우선 1개의 파라미터에 대해서만 미분을 하자’ 라는 목적으로 다른 변수들을 상수 취급 하는 방법이다.
  • ex) $f(x,y) = x^2 + 4xy + 9y^2$라는 함수의 $f’(1, 2)$의 값을 계산할 때,
  • 이를 위해서 해야 하는 것은,
    1. $x$에 대해 편미분
      • $\partial f(x,y) \over \partial x$ = $2x + 4y$
      • ${f’(1, 2) \over \partial x}$ = $2 \cdot (1) + 4 \cdot (2) = 10$
    2. $y$에 대해 편미분
      • $\partial f(x,y) \over \partial y$ = $4x + 18y$
      • ${f’(1, 2) \over \partial y}$ = $4 \cdot 1 + 18 \cdot 2 = 40$

Chain Rule

  • 함수의 함수를 미분하기 위해 사용하는 방식으로, 합성함수라고 부르기도 한다.
  • 공식
    • $F(x) = f(g(x))$
    • $F’(x)$ $\rightarrow$ $f’((g(x)) \cdot g’(x)$
  • 예제
    • $F(x) = (2x^3 + 7)^6$ 를 x에 대해 미분하려는 경우
    • $f(x) = x^6, g(x) = 2x^3 + 7$로 설정
    • $F’(x) = 6(2x^3 + 7)^5 \cdot 6x^2$

미분의 실사용 예시

경사하강법(Gradient Descent)

  • 오차 함수인 𝜀(엑설런)을 최소화 하는 𝑎,𝑏 를 찾을 수 있는 최적화 알고리즘 중의 하나이다.
  • 최적의 $a, b$를 찾기 위해선 미분계수가 0인 곳을 찾으면 된다.
  • 하지만 현실적으로 파라미터의 갯수는 수 없이 많을 것이고 하나의 minimum/maximum만이 존재하지 않는 상황에 직면하게 될 것이다.
  • 경사하강법은 임의의 a, b를 선택한 후(random initialization)에 기울기 (gradient)를 계산해서 기울기 값이 낮아지는 방향으로 진행된다.
  • 기울기는 항상 손실 함수 값이 가장 크게 증가하는 방향으로 진행한다.
  • 그렇기 때문에 경사하강법 알고리즘은 기울기의 반대 방향으로 이동한다.
    • $a_{n+1} = a_n - \eta ∇ f(a_n)$
    • $b_{n+1} = b_n - \eta ∇ f(b_n)$
  • 반복적으로 파라미터 $a, b$를 업데이트 해가면서 그래디언트($∇ f$)가 0이 될 때까지 이동한다.
  • 이 때 중요한 것은 학습률(learning rate, $\eta$)이다.
  • 학습률이 너무 낮으면 알고리즘이 수렴하기 위해서 반복을 많이 해야되고 이는 결국 수렴에 시간을 상당히 걸린다.
  • 반대로 학습률이 너무 크면 오히려 극소값을 지나쳐 버려서 알고리즘이 수렴을 못하고 계산을 계속 반복하게 될 수도 있기 때문에 학습률은 신중하게 정해야 한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def gradient_descent(X, y, lr = 0.05, epoch = 10):
    
    a, b = 0.33, 0.48 # 임의 선택한 파라미터 a, b
    N = len(X) # 샘플 갯수
    
    for _ in range(epoch):            
        f = y - (a*X + b)
    
        # a와 b를 업데이트
        a -= lr * (-2 * X.dot(f).sum() / N)
        b -= lr * (-2 * f.sum() / N)        
        
    print('a: '+str(a))
    print('b: '+str(b))
    
    # y = 3 x + 5
X = np.array([1, 2, 3, 4, 5])
y = np.array([8, 11, 14, 17, 20])

gradient_descent(X,y)  # 10번만 돌렸을 때

# a: 3.820070615328
# b: 2.0392842721280005

gradient_descent(X, y, epoch = 1000)  # 1000번 반복

# a: 3.000000038323629
# b: 4.999999861639539
  • 점점 a = 3, b = 5로 수렴한다.
0%