머신러닝(Machine Learning)

AI는 머신러닝(Machine Learning)과 머신러닝의 한 갈래인 딥러닝(Deep Learning)을 의미한다.
머신러닝은 이미지 인식, 영상 처리, 알파고와 같은 분야 뿐만 아니라 자연어 처리에 있어서도 유용하게 쓰인다.
특히 머신러닝의 한 갈래인 딥러닝은 기존의 통계 기반에서 접근했던 자연어 처리의 성능을 훨씬 뛰어 넘는 성능을 보이고 있어, 현재에 이르러서는 자연어 처리에 있어 딥러닝은 필수가 되었다.

머신러닝이란?

머신러닝이 아닌 접근 방법의 한계

기존의 프로그래밍 접근 방법으로 고양이나 강아지를 판별하기 어렵다.
애초에 숫자를 정렬하는 것과 같은 명확한 알고리즘이 애초에 존재하지 않는다.

머신러닝은 기존 프로그래밍의 한계에 대한 해결책

머신러닝 톺아보기

머신러닝모델의 평가

실제 모델을 평가하기 위해서 데이터를 훈련용, 검증용, 테스트용 이렇게 세 가지로 분리하는 것이 일반적이다.
검증용 데이터는 모델의 성능을 평가하기 위한 용도가 아니라, 모델의 성능을 조정하기 위한 용도이다.
- 과적합이 되고 있는지 판단하거나 하이퍼파라미터의 조정을 위한 용도이다.
하이퍼파라미터(초매개변수)란 값에 따라서 모델의 성능에 영향을 주는 매개변수이다.
가중치와 편향과 같은 학습을 통해 바뀌어져가는 변수는 매개변수이다.
하이퍼파라미터와 매개변수의 가장 큰 차이는 하이퍼파라미터는 보통 사용자가 직접 정해줄 수 있는 변수이다.
하이퍼파라미터는 사람이 정하는 변수인 반면, 매개변수는 기계가 훈련을 통해서 바꾸는 변수이다.
훈련용 데이터로 훈련을 모두 시킨 모델은 검증용 데이터를 사용하여 정확도를 검증하며 하이퍼파라미터를 튜닝(tuning)한다.
이 모델의 매개변수는 검증용 데이터로 정확도가 검증되는 과정에서 점차 검증용 데이터에 점점 맞추어져 가기 시작한다.
검증이 끝났다면 테스트 데이터를 가지고 모델의 진짜 성능을 평가한다.
훈련 데이터는 문제지, 검증 데이터는 모의고사, 테스트 데이터는 실력을 최종적으로 평가하는 수능 시험을 예시로 들 수 있다.

분류(Classification)와 회귀(Regression)

선형 회귀를 통해 회귀 문제에 대해서 학습한다.
로지스틱 회귀를 통해 (이름은 회귀이지만) 분류 문제를 학습한다.

1. 이진 분류 문제(Binary Classification)

주어진 입력에 대해서 둘 중 하나의 답을 정하는 문제이다.
- 예) 시험 성적에 대해서 합격, 불합격인지 판단하고 메일로부터 정상 메일, 스팸 메일인지를 판단하는 문제

2. 다중 클래스 분류(Multi-class Classification)

주어진 입력에 대해서 두 개 이상의 정해진 선택지 중에서 답을 정하는 문제이다.
- 예) 서점 아르바이트를 하는데 과학, 영어, IT, 학습지, 만화라는 레이블이 각각 붙여져 있는 5개의 책장이 있다. 새 책이 입고되면, 이 책은 다섯 개의 책장 중에서 분야에 맞는 적절한 책장에 책을 넣어야 한다. 이 때의 다섯 개의 선택지를 주로 카테고리 또는 범주 또는 클래스라고 하며, 주어진 입력으로부터 정해진 클래스 중 하나로 판단하는 것을 다중 클래스 분류 문제라고 한다.

3. 회귀 문제(Regression)

분류 문제처럼 0 또는 1이나 과학 책장, IT 책장 등과 같이 분리된(비연속적인) 답이 결과가 아니라 연속된 값을 결과로 가진다.
- 예) 예를 들어 시험 성적을 예측하는데 5시간 공부하였을 때 80점, 5시간 1분 공부하였을 때는 80.5점, 7시간 공부하였을 때는 90점 등이 나오는 것과 같은 문제가 있다. 그 외에도 시계열 데이터를 이용한 주가 예측, 생산량 예측, 지수 예측 등이 이에 속한다.

지도 학습(Supervised Learning)과 비지도 학습(Unsupervised Learning)

1. 지도 학습

레이블(Label)이라는 정답과 함께 학습하는 것이다.
$y$, 실제값 등으로 부르기도 한다.
이때 기계는 예측값과 실제값의 차이인 오차를 줄이는 방식으로 학습을 하게 되는데 예측값은 $\hat{y}$과 같이 표현하기도 한다.

2. 비지도 학습

레이블이 없이 학습하는 것이다.
예) 클러스터링

샘플(Sample)과 특성(Feature)

많은 머신러닝 문제가 1개 이상의 독립 변수 $x$를 가지고 종속 변수 $y$를 예측하는 문제이다.
많은 머신러닝 모델들, 특히 인공 신경망 모델은 독립 변수, 종속 변수, 가중치, 편향 등을 행렬 연산을 통해 연산하는 경우가 많다.

위 이미지는 독립 변수 $x$의 행렬을 $X$라고 하였을 때, 독립 변수의 개수가 $n$개이고 데이터의 개수가 $m$인 행렬 $X$이다.
이때 머신러닝에서는 하나의 데이터, 하나의 행을 샘플(Sample)이라고 부른다.
(데이터베이스에서는 레코드라고 부르는 단위)
종속 변수 $y$를 예측하기 위한 각각의 독립 변수 $x$를 특성(Feature)이라고 부른다.

선형 회귀(Linear Regression)

어떤 변수의 값에 따라서 특정 변수의 값이 영향을 받는다.
변수의 값을 변하게하는 변수를 $x$, 변수 $x$에 의해서 값이 종속적으로 변하는 변수 $y$라고 할 때, 변수 $x$의 값은 독립적으로 변할 수 있는 것에 반해, $y$값은 계속해서 $x$의 값에 의해서, 종속적으로 결정되므로 $x$를 독립 변수, $y$를 종속 변수라고 한다.
선형 회귀는 한 개 이상의 독립 변수 $x$와 $y$의 선형 관계를 모델링한다. 만약, 독립 변수 $x$가 1개라면 단순 선형 회귀라고 한다.

주택 판매 가격 예측

import pandas as pd
# 주어진 url 주소를 이용해 house prices 데이터 import
df = pd.read_csv('https://ds-lecture-data.s3.ap-northeast-2.amazonaws.com/house-prices/house_prices_train.csv')
df_t = pd.read_csv('https://ds-lecture-data.s3.ap-northeast-2.amazonaws.com/house-prices/house_prices_test.csv')

df.head()
df_t.head()

# 여러 특성 중 'GrLivArea', 'LotArea', 'SalePrice'를 사용
# SalePrice: 예측해야 하는 타겟값으로 주택판매가격(달러)
# LotArea: 집과 마당의 사이즈(square feet)
# GrLivArea: 지상 생활면적(square feet)
df = df[['GrLivArea', 'LotArea', 'SalePrice']]
df_t = df_t[['GrLivArea', 'LotArea']]

# 테이블 형태 출력, 이런 형태의 데이터: tabular data
# 특징 3가지
# Observations: 테이블의 행의 위치
# Variables: 테이블의 열에 위치
# Relationship: 한 테이블의 데이터를 다음과 연결
df

예측 방법

1. 기존 경험을 바탕으로 예측

대충 어림짐작하는 것이다.
보통 좋은 결과를 내기도 하지만, 사람마다 편견이 존재하며 오류에 빠질 위험이 높다.

2. 통계 정보를 활용

# SalePrice의 통계 정보
df['SalePrice'].describe()

'''
count     1,460.0
mean    180,921.2
std      79,442.5
min      34,900.0
25%     129,975.0
50%     163,000.0
75%     214,000.0
max     755,000.0
Name: SalePrice, dtype: float64
'''

import matplotlib.pyplot as plt
import seaborn as sns

## SalePrice의 확률밀도함수
sns.displot(df['SalePrice'], kde=True)

## 평균과, 중간값 수직선
plt.axvline(df['SalePrice'].mean(), color='blue')
plt.axvline(df['SalePrice'].median(), color='red');

만일 가격을 처음으로 예측할 때, 가장 간단하고 직관적인 방법으로 평균이나 중간값을 이용해 보는 것도 좋은 선택일 것이다.

기준 모델(Baseline Model)

베이스라인 모델은 예측 모델을 구체적으로 만들기 전에 가장 간단하면서도 직관적이면서 최소한의 성능을 나타내는 기준이 되는 모델이다.
평균값을 기준으로 사용하면 ‘평균 베이스라인 모델’이다.
문제별로 기준 모델은 다음과 같이 설정한다.
- 분류 문제: 타겟의 최빈 클래스
- 회귀 문제: 타겟의 평균값
- 시계열 회귀 문제: 이전 타임 스탬프의 값

# predict: 직접 정한 기준모델인 평균으로 예측
predict = df['SalePrice'].mean()

# 평균값으로 예측할 때 샘플 별 평균값과의 차이(error)를 저장
errors = predict - df['SalePrice']

errors

'''
0      -27,578.8
1         -578.8
2      -42,578.8
3       40,921.2
4      -69,078.8
          ...   
1455     5,921.2
1456   -29,078.8
1457   -85,578.8
1458    38,796.2
1459    33,421.2
Name: SalePrice, Length: 1460, dtype: float64
'''

# mean_absolute_error(MAE), error에 절대값을 취한 후 평균을 계산
mean_absolute_error = errors.abs().mean()

MAE(Mean Absolute Error, 평균 절대 오차)는 예측 에러의 절대값 평균을 나타낸다.

\[Error = (price - guess)\] \[\begin{align}mae = (\frac{1}{n})\sum_{i=1}^{n}\left | price_{i} - guess_{i} \right |\end{align}\]

MSE, MAE의 차이

MSE는 제곱을 해주고, MAE는 제곱은 하지 않고 절대값을 구한다.

평균 제곱 오차(MSE)는 회귀에서 자주 사용되는 손실 함수로써 정확도 개념은 회귀에 적용되지 않는다.

일반적인 회귀 지표는 평균 절대 오차(MAE)이다.

MSE는 손실 함수로써 쓰인다.

MAE는 회귀 지표로써 쓰인다.

# 베이스라인 모델 시각화
x = df['GrLivArea']
y = df['SalePrice']

predict = df['SalePrice'].mean()
errors = predict - df['SalePrice']
mean_absolute_error = errors.abs().mean()

sns.lineplot(x=x, y=predict, color='red')
sns.scatterplot(x=x, y=y, color='blue');

print(f'예측한 주택 가격이 ${predict:,.0f}이며 절대평균에러가 ${mean_absolute_error:,.0f}임을 확인할 수 있습니다.')
'''
예측한 주택 가격이 $180,921이며 절대평균에러가 $57,435임을 확인할 수 있습니다.
'''

평균예측은 에러가 상당히 크다.

# 주택 가격이 전체 공간 크기(LotArea)와 같은 다른 특성과 어떤 상관관계(dependent)가 있는 지 확인

sns.set(style='whitegrid', context='notebook')
cols = ['GrLivArea', 'LotArea','SalePrice']
sns.pairplot(df[cols], height=2);

3. 예측 모델(Predictive Model) 활용

스캐터 플롯(Scatter plot)에 가장 잘 맞는(Base fit) 직선을 그려주면 그것이 회귀 예측 모델이 된다.

회귀 직선을 만드는 방법

회귀 분석에서 중요한 개념은 예측값과 잔차(Residual)이다.
- 예측값은 만들어진 모델이 추정하는 값이다.
- 잔차는 예측값과 관측값의 차이이다.
  (오차(Error)는 모집단에서의 예측값과 관측값의 차이를 뜻한다.)
회귀선은 잔차 제곱들의 합인 RSS(Residual sum of Squares)를 최소화하는 직선이다ㅏ.
- RSS: SSE(Sum of Square Error)라고도 말하며 이 값이 회귀 모델의 비용함수(Cost Function)가 된다.
머신러닝에서는 비용함수를 최소화하는 모델을 찾는 과정을 학습이라고 한다.

\[{\displaystyle \operatorname {RSS} =\sum _{i=1}^{n}(\varepsilon _{i})^{2}=\sum _{i=1}^{n}(y_{i}-f(x_{i}))^{2}=\sum _{i=1}^{n}(y_{i}-(\alpha x_{i} + \beta))^{2}}\]

여기서 계수 $a$와 $b$는 RSS를 최소화하는 값으로 모델 학습을 통해 얻어지는 값이다.
잔차 제곱합을 최소화하는 방법을 최소 제곱 회귀 또는 OLS(Ordinary Least Squares)라고 부른다.
OLS는 계수 계산을 위해 다음 공식을 사용한다.

\[\beta =\displaystyle {\bar {y}}-\alpha{\bar {x}}\] \[\alpha ={\frac {S_{xy}}{S_{xx}}}\] \[{\displaystyle S_{xy}=\sum _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}\] \[{\displaystyle S_{xx}=\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}\]

최소제곱법으로 선형 회귀계수를 쉽게 구할 수 있다.

# Seaborn regplot으로 그리면, 
sns.regplot(x=df['GrLivArea'], y=df['SalePrice']);

# GrLivArea > 3500 & GrLivArea < 4500 사이의 데이터
df[(df['GrLivArea'] > 3500) & (df['GrLivArea'] < 4500)]

선형 회귀는 주어져 있지 않은 점의 함수값을 보간(Interpolate)하여 예측하는데 도움을 준다.
선형 회귀 모델을 사용해 4000sqft 주택 가격을 어림잡아 예측해 볼 수 있다.
선형 회귀 모델은 기존 데이터의 범위를 넘어서는 값을 예측하기 위한 외삽(Extrapolate)도 제공한다.
현재 다루는 데이터에 6000sqft 이상인 주택의 거래 정보가 없다.

이런 경우 예측하는 방법

선형 회귀 직선은 독립변수(Independent Variable, $x$)와 종속변수(Dependent Variable, $y$) 간의 관계를 요약해준다.
- 종속변수
  - 연구자가 독립변수의 변화에 따라 어떻게 변하는지 알고 싶어하는 변수이다.
  - 반응변수(Response), 레이블(Label), 타겟(Target) 등
- 독립변수
  - 연구자가 의도적으로 변화시키는 변수이다.
  - 다른 변수에 영향을 받지 않고 오히려 종속변수에 영향을 준다.
  - 예측변수(Predictor), 설명(Explanatory), 특성(Feature) 등

사이킷런(Scikit-Learn) 활용 선형 회귀 모델

사이킷런은 머신러닝 모델을 만드는데 가장 많이 사용되는 라이브러리이다.

사이킷런 데이터 구조

사이킷런을 활용해 모델을 만들고 데이터를 분석하기 위해서는 위와 같은 구조를 사용해야 한다.
특정 데이터와 타겟 데이터를 나누어 준다.
특성행렬은 주로 X로 표현하고 보통 2차원 행렬이다.
- 주로 넘파이(Numpy) 행렬이나 판다스(Pandas) 데이터 프레임으로 표현한다.
타겟배열은 주로 y로 표현하고 보통 1차원 형태이다.
- 주로 넘파이 행렬이나 판다스 데이터 프레임으로 표현한다.

수많은 머신러닝 모델

모두 유사한 프로세스를 통해서 사용할 수 있다.
적합한 모델을 선택하여 클래스를 찾아본 후 관련 속성이나 하이퍼파라미터를 확인한다.
fit() 메소드를 사용하여 모델 학습을 진행한다.
predict() 메소드를 사용하여 새로운 데이터를 예측한다.

단순 선형 회귀(Simple Linear Regression)

# Scikit-Learn 라이브러리에서 사용할 예측모델 클래스 Import
from sklearn.linear_model import LinearRegression


# 예측모델 인스턴스
model = LinearRegression()


# X 특성들의 테이블과, y 타겟 벡터 생성
feature = ['GrLivArea']
target = ['SalePrice']
X_train = df[feature]
y_train = df[target]


# 모델학습(fit)
model.fit(X_train, y_train)
'''
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
'''


# 새로운 데이터 한 샘플을 선택해 학습한 모델을 통해 예측
X_test = [[4000]]
y_pred = model.predict(X_test)

print(f'{X_test[0][0]} sqft GrLivArea를 가지는 주택의 예상 가격은 ${int(y_pred)} 입니다.')
'''
4000 sqft GrLivArea를 가지는 주택의 예상 가격은 $447090 입니다.
'''


# 전체 테스트 데이터를 모델을 통해 예측
X_test = [[x] for x in df_t['GrLivArea']]
y_pred = model.predict(X_test)


# 전체 예측값
y_pred
'''
array([[114557.82748987],
       [160945.27292207],
       [193084.38061182],
       ...,
       [149696.58523066],
       [122485.47405334],
       [232829.74378814]])
'''


# train 데이터와 예측에 대한 그래프
plt.scatter(X_train, y_train, color='black', linewidth=1)
plt.scatter(X_test, y_pred, color='blue', linewidth=1);

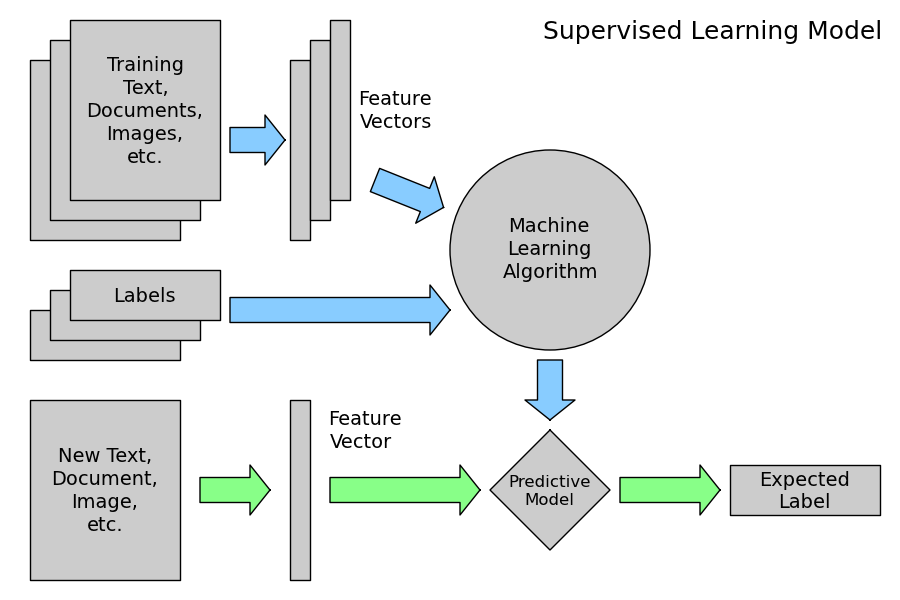
위 코드는 이 다이어그램에서 표현한 일반적인 머신러닝 프로세스를 수행했다.
파란색은 학습, 초록색은 테스트를 뜻한다.

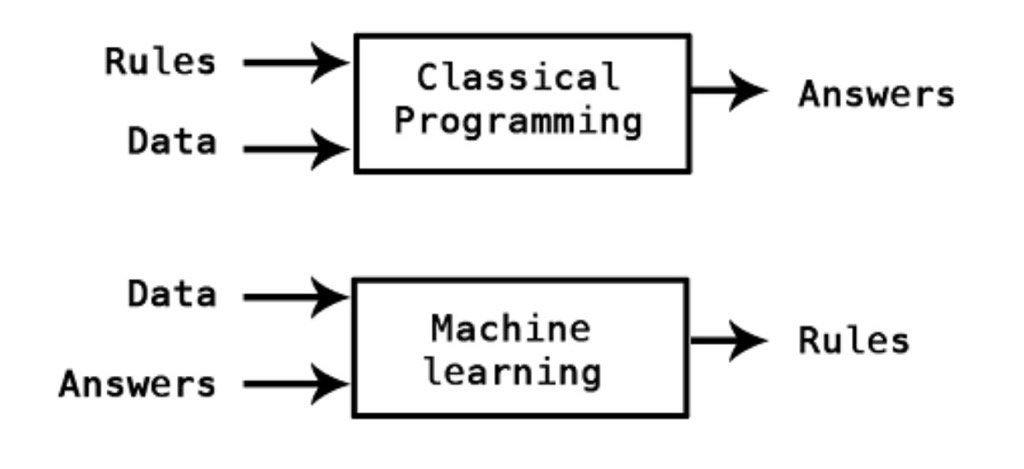
머신러닝을 새로운 프로그래밍 패러다임으로 바라볼 수도 있다.
데이터를 입력하고 어떤 룰에 따라 답을 구해내는 일반적인 프로그래밍과 달리 머신러닝은 데이터와 답을 통해 룰을 찾아내는 방법이다.

계수(Coefficients)

모델이 주택의 크기와 가격 사이의 어떤 관계를 학습했는지 보기 위해 LinearRegression 객체의 coef_, intercept_ 속성을 확인한다.

# 계수(coefficient)
model.coef_
'''
array([[107.13035897]])
'''


# 절편(intercept)
model.intercept_
'''
array([18569.02585649])
'''

계수의 영향

예측함수를 만들어 새로운 데이터를 반복해서 예측하고 계수의 영향을 설명한다.

def explain_prediction(sqft):
    y_pred = model.predict([[sqft]])
    pred = f"{int(sqft)} sqft 주택 가격 예측: ${int(y_pred[0])} (1 sqft당 추가금: ${int(model.coef_[0])})"

    return pred


# square_feet = 4000 인 테스트 데이터로 예측
print(explain_prediction(4000))
'''
4000 sqft 주택 가격 예측: $447090 (1 sqft당 추가금: $107)
'''

ipywidgets 사용

sqft를 바꾸어가며 예측해본다.

from ipywidgets import interact


# 데코레이터 interact를 추가
@interact
def explain_prediction(sqft=(500,10000)):
    y_pred = model.predict([[sqft]])
    pred = f"{int(sqft)} sqft 주택 가격 예측: ${int(y_pred[0])} (1 sqft당 추가금: ${int(model.coef_[0])})"

    return pred

선형 회귀 모델을 만들기 위한 좋은 특성

선형성
- 선형은 회귀 분석에서 중요한 기본과정이다.
- 예측하고자 하는 종속변수 y와 독립변수 x간에 선형성을 만족하는 특성이다.
- 독립 변수들에 대해 편미분을 하면 상수가 나와야 한다.
- 선형성을 만족하지 않는 문제를 해결하는 방법으로,
- 다른 새로운 변수를 추가하거나
- 로그, 지수, 루트 등 변수 변환을 취해보거나
- 아예 선형성을 만족하지 않는 변수를 제거하거나
- 일단 선형 회귀 모델을 만들고 변수 선택법을 통과시키는 것 등이 있다.
독립성
- 독립성은 다중 회귀 분석에서 중요한 기본 가정으로, 당연히 단순 회귀 분석에서는 해당하지 않는다.
- 독립변수 x 간에 상관 관계가 없이 독립성을 만족하는 특성이다.
- 두 개의 서로 다른 시점의 오차항 사이에 공분산이 0이어야 한다.
등분산성
- 등분산성이란 분산이 같다는 것이고, 분산이 같다는 것은 특정한 패턴 없이 고르게 분포했다는 의미이다.
- 어느 시점에서 관측하더라도 동일한 분산이 나와야한다.
정규성
- 마지막 정규성은 잔차가 정규성을 만족하는지 여부로, 정규 분포를 띄는지 여부를 의미한다.
가우스 마코프 정리의 조건 만족
- 가우스 마코프 정리: 특정 가정/조건을 만족할 경우, 우리가 구한 최소 제곱 추정량(OLS의 추정량)이 BLUE(Best Linear Unbiased Estimator)이다.
  가장 좋은 회귀모형을 만들 수 있다 생각하면 된다.
  BLUE: 추정치 중 가장 좋은 불편 추정

최소자승법(OLS, Ordinary Least Squares)

잔차 제곱합(RSS)를 최소화하는 가중치(단순선형 회귀에서는 기울기, 회귀계수)를 구하는 방법이다.
통계를 처음 배울 때 가장 접하게 되면서 단순하면서 가장 많이 쓰이는 방법이다.
선형 회귀 모델의 추정방법 중에 하나이지만 선형 회귀 모델 자체는 아니다.
데이터의 추세선을 그리고 싶을 때 쓰는 방법이다.
잔차의 제곱의 합을 최소로 하는 방법이다.

[머신러닝] 선형 회귀(Linear Regression)란?