역전파 미적분

(필기노트 제공 by Crystal Yim in CS AIB 5th)

Neural Networks Demystified

신경망 구조(recap.)

신경망의 학습: 적절한 가중치를 찾아가는 과정
HOW?
- Gradient descent, Backpropagation!
경사 하강법에 필요한 Gradient 계산을 역전파 알고리즘을 통해 구한다.

신경망에는 3개의 Layer가 존재한다.
각 층은 Node로 구성되어 있으며, 각 노드는 Weight, Bias로 연결되어 있다.
순전파: 입력층에서 입력된 신호가 은닉층의 연산을 거쳐 출력층에서 값을 내보내는 과정
- 입력층으로부터 신호를 전달
- 입력된 데이터를 가중치 및 편향과 연산한 뒤 더해준다.(가중합, Weighted Sum)
- 가중합을 통해 구해진 값은 Activation func을 통해 다음 층으로 전달
특정 층에 입력되는 데이터의 특성의 $n$개인 경우 수식으로 나타낸다면,(Sigmoid)

\[y = \text{sigmoid}\bigg(\sum( b + w_{1}x_{1} + w_{2}x_{2} + ... + w_{n}x_{n})\bigg)\]

신경망 학습 알고리즘 요약

데이터와 목적에 맞게 신경망 구조 설계
- Input node: 데이터 Feature 수
- Output node: 문제에 따라 다르게 설정
- Hidden과 node 수 결정
Weight Random 초기화
순전파를 통해 출력값($h_{\theta}(x^{(i)})$)을 모든 입력 데이터($x^{(i)}$)에 대해 계산
Cost func($J(\theta)$) 계산
역전파를 통해 각 가중치에 대해 편미분 값($\partial J(\theta)/\partial\theta_{jk}^{l}$)을 계산
경사하강법을 사용하여 비용함수($J(\theta)$)를 최소화하는 방향으로 가중치를 갱신
중지 기준을 충족하거나 비용함수를 최소화 할 때까지 2-5단계 반복(iteration)

Cost Func or Loss Func

신경망은 Loss func를 최소화하는 방향으로 weight을 갱신
Loss func을 잘 정의해주어야 weight이 제대로 갱신
입력 데이터를 신경망에 넣어 순전파를 거치면 마지막 출력층을 통과한 값이 도출
출력된 값과 그 데이터의 타겟값을 손실함수에 넣어 손실(Loss or Error)를 계산
한 데이터 포인트에서의 손실을 Loss라고 하며, 전체 데이터셋의 Loss를 합한 개념을 Cost라고 한다.
대표적 손실함수: MSE, Cross-Entropy
신경망 학습에는 머신러닝 알고리즘보다 많은 훈련 데이터가 필요
그에 따라 시간도 오래 걸리고 최적화를 위해 더 많은 Hyperparameter tuning을 해주어야한다.
복잡한 신경망을 훈련하기 위해 특별한 방법이 바로 Backpropagation Algorithm

Backpropagation

Backwards Propagation of Errors의 줄임말
순전파와는 반대 방향으로 Loss of Error 정보를 전달해주는 역할
순전파가 입력 신호 정보를 입력층부터 출력층까지 전달하여 값을 출력하는 알고리즘이라면,
역전파는 구해진 손실 정보를 출력층부터 입력층까지 전달하여 각 가중치를 얼마나 업데이트 해야할지를 결정하는 알고리즘
매 iteration 마다 구해진 Loss를 줄이는 방향으로 가중치 업데이트
손실을 줄이는 방향을 결정하는 것이 Gradient Descent
GD와 BP를 이해하기 위해서는 미분법에 대한 이해가 필요하다.

Exemple

공부시간, 수면시간을 특성으로 하고 시험 점수를 레이블로 하는 회귀 예제
$x_1$ 은 공부시간을 나타내고 $x_2$ 는 수면시간

\[y = 5x_1 + 2x_2 + 40\]

import numpy as np

np.random.seed(812)


# 특성 데이터로부터 관계를 만족하는 레이블 도출한 뒤 데이터셋 생성

x = np.array(([8, 8],
              [2, 5],
              [7, 6]), dtype = float)

# 시험 점수 레이블 생성
y = X[:,0]*5 + X[:,1]*2
y = y.reshape(3,1)


# Normalization
X = X / np.amax(X, axis=0)
y = y / np.amax(y, axis=0)

print("공부시간, 수면시간 \n", X)
print("시험점수 \n", y)
'''
공부시간, 수면시간 
 [[1.    1.   ]
 [0.25  0.625]
 [0.875 0.75 ]]
시험점수 
 [[1.        ]
 [0.35714286]
 [0.83928571]]
'''


# NeuralNetwork 클래스 내 __init__ 메소드(함수)에서 신경망을 구축
class NeuralNetwork:
    """
    신경망(Neural network)를 정의하는 클래스(Class) 선언
    """
    def __init__(self):
        """
        신경망의 구조를 결정합니다.

        inputs : 입력층 노드 수
        hiddenNodes : 은닉층 노드 수
        outputNodes : 출력층 노드 수
        w1, w2 : 은닉층(layer 1), 출력층(layer 2)의 가중치
        """
        
        self.inputs = 2
        self.hiddenNodes = 3
        self.outputNodes = 1
        
        # 가중치 초기화
        # layer 1 가중치 shape : 2x3
        self.w1 = np.random.randn(self.inputs,self.hiddenNodes)
        
        # layer 2 가중치 shape : 3x1
        self.w2 = np.random.randn(self.hiddenNodes, self.outputNodes)

# 정의된 클래스 사용, 해당 가중치 디스플레이
nn = NeuralNetwork()

print("Layer 1 가중치: \n", nn.w1)
print("Layer 2 가중치: \n", nn.w2)
'''
Layer 1 가중치: 
 [[ 2.48783189  0.11697987 -1.97118428]
 [-0.48325593 -1.50361209  0.57515126]]
Layer 2 가중치: 
 [[-0.20672583]
 [ 0.41271104]
 [-0.57757999]]
'''

행렬의 곱셈 연산

$A_{l \times m}, B_{m \times n}$ 두 행렬을 곱할 때 $\Rightarrow (AB)_{l \times n}$
결과값으로 나오는 행렬의 shape은 $\big($$l$ $\times$ $m$$\big)$ $\cdot$ $\big($ $m$ $\times$ $n$ $\big)$ = $l$ $\times$ $n$ 행렬의 형태로 연산

# 순전파 기능 추가 구현
class NeuralNetwork:
    
    def __init__(self):
        """
        신경망의 구조를 결정합니다.

        inputs : 입력층 노드 수
        hiddenNodes : 은닉층 노드 수
        outputNodes : 출력층 노드 수
        w1, w2 : layer 1, layer 2의 가중치
        """
        self.inputs = 2
        self.hiddenNodes = 3
        self.outputNodes = 1
        
        # 가중치를 초기화 합니다.
        # layer 1 가중치 shape : 2x3
        self.w1 = np.random.randn(self.inputs,self.hiddenNodes)
        
        # layer 2 가중치 shape : 3x1
        self.w2 = np.random.randn(self.hiddenNodes, self.outputNodes)
        
    def sigmoid(self, s):
        """
        활성화 함수인 시그모이드 함수를 정의합니다.
        s : 활성화 함수에 입력되는 값(=가중합)
        """
        return 1 / (1+np.exp(-s))
    
    def feed_forward(self, X):
        """
        순전파를 구현합니다.
        입력 신호를 받아 출력층의 결과를 반환합니다.
        
        hidden_sum : 은닉층(layer 1)에서의 가중합(weighted sum)
        activated_hidden : 은닉층(layer 1) 활성화 함수의 함숫값
        output_sum : 출력층(layer 2)에서의 가중합(weighted sum)
        activated_output : 출력층(layer 2) 활성화 함수의 함숫값
        """
        
        self.hidden_sum = np.dot(X, self.w1)
        self.activated_hidden = self.sigmoid(self.hidden_sum)

        self.output_sum = np.dot(self.activated_hidden, self.w2)
        self.activated_output = self.sigmoid(self.output_sum)
        
        return self.activated_output


# 순전파 거쳐 출력되는 값
nn = NeuralNetwork()
print(X[0])
'''
[1. 1.]
'''


# 신경망 출력값 확인
output = nn.feed_forward(X[0])
print("예측값: ", output)
'''
예측값:  [0.21945787]
'''


# Error or Loss Cost
error = y[0] - output
error
'''
array([0.78054213])
'''


# 모든 과정
output_all = nn.feed_forward(X)
error_all = y - output_all
'''
[[0.78054213]
 [0.0114108 ]
 [0.6013965 ]]
'''

분석

에러가 높게 나온 이유: 예측값이 정확하지 않기 때문
예측값이 정확하지 않은 이유: 임의로 지정하였던 가중치 값이 작거나, 첫번째 층의 출력값이 작기 때문
첫번재 층의 출력값이 작은 이유: 입력 데이터는 변하지 않는 값이므로 첫번째 층의 가중치 값이 작기 때문
예측값을 증가시키기 위한 방법: 첫번째 층과 두번째 층의 가중치를 증가시키는 것

# 각 층의 가중치
attributes = ['w1', 'hidden_sum', 'activated_hidden', 'w2', 'activated_output']

for i in attributes:
    if i[:2] != '__':
        print(i+'\n', getattr(nn,i), '\n'+'---'*3)
'''
w1
 [[-1.75351135  1.23279898  0.24464757]
 [-0.06568225  0.30190098  0.79723428]] 
---------
hidden_sum
 [[-1.8191936   1.53469996  1.04188185]
 [-0.47942924  0.49688786  0.55943332]
 [-1.58358412  1.30512484  0.81199233]] 
---------
activated_hidden
 [[0.13953066 0.82269293 0.73921295]
 [0.38238691 0.62172769 0.63632141]
 [0.17028848 0.78669622 0.6925339 ]] 
---------
w2
 [[ 1.23073545]
 [-1.52187331]
 [-0.25502715]] 
---------
activated_output
 [[0.21945787]
 [0.34573206]
 [0.23788921]] 
---------
'''

HOW?

Error를 줄이기 위해서 어떻게 해야할까?
Cost func $J$의 Gradient가 작아지는 방향으로 업데이트하면 손실함수의 값을 줄일 수 있다.
매 iteration마다 해당 가중치에서의 Cost func의 도함수(미분한 함수)를 계산하여 경사가 작아지도록 가중치를 변경한다.

위의 신경망은 총 9개의 가중치를 가졌다.
첫 번째 층에는 6개(w1), 두 번째 층에는 3개(w2)
해당 신경망의 비용 함수는 9차원 공간상의 함수$(J)$
비용 함수 $J$를 수식으로 나타내면,

\[J(\theta) = J(\theta_1, \theta_2, \theta_3, \theta_4, \theta_5, \theta_6, \theta_7, \theta_8, \theta_9)\]

Convex/Concave func과 Local Optima

경사 하강법을 통해 최저점을 찾는 메커니즘은 Convex func에서만 잘 동작
실제 손실 함수는 위 그림처럼 Convex, Concave가 공존
So, Global Optima를 찾지 못하고 Local Optima에 빠질 수 있다.
- 그래서 또 방지하는 법이 있지.

Update weight: BP

# 역전파 기능 구현
# 음수 가중치를 가지는 활성화는 낮추고, 양수 가중치를 가지는 활성화는 높인다.
class NeuralNetwork:
    
    def __init__(self):
        """
        신경망의 구조를 결정합니다.

        inputs : 입력층 노드 수
        hiddenNodes : 은닉층 노드 수
        outputNodes : 출력층 노드 수
        w1, w2 : layer 1, layer 2의 가중치
        """
        self.inputs = 2
        self.hiddenNodes = 3
        self.outputNodes = 1
        
        # 가중치를 초기화 합니다.
        # layer 1 가중치 shape : 2x3
        self.w1 = np.random.randn(self.inputs,self.hiddenNodes)
        
        # layer 2 가중치 shape : 3x1
        self.w2 = np.random.randn(self.hiddenNodes, self.outputNodes)
        
    def sigmoid(self, s):
        """
        활성화 함수인 시그모이드 함수를 정의합니다.
        s : 순전파 과정에서 활성화 함수에 입력되는 값(=가중합)
        """
        return 1 / (1+np.exp(-s))

    def sigmoidPrime(self, s):
        """
        활성화 함수(sigmoid)를 미분한 함수입니다.
        s : 순전파 과정에서 활성화 함수에 입력되는 값(=가중합)
        """
        sx = self.sigmoid(s)
        return sx * (1-sx)
    
    def feed_forward(self, X):
        """
        순전파를 구현합니다.
        입력 신호를 받아 출력층의 결과를 반환합니다.
        
        hidden_sum : 은닉층(layer 1)에서의 가중합(weighted sum)
        activated_hidden : 은닉층(layer 1) 활성화 함수의 함숫값
        output_sum : 출력층(layer 2)에서의 가중합(weighted sum)
        activated_output : 출력층(layer 2) 활성화 함수의 함숫값
        """
        
        self.hidden_sum = np.dot(X, self.w1)
        self.activated_hidden = self.sigmoid(self.hidden_sum)

        self.output_sum = np.dot(self.activated_hidden, self.w2)
        self.activated_output = self.sigmoid(self.output_sum)
        
        return self.activated_output
    
    def backward(self, X, y, o):
        """
        역전파를 구현합니다.
        출력층에서 손실 값(Error)를 구한 뒤에 이를 각 가중치에 대해 미분한 값만큼 가중치를 수정합니다.

        X : 입력 데이터(input)
        y : 타겟값(target value)
        o : 출력값(output)

        o_error : 손실(Error) = 타겟값과 출력값의 차이
        o_delta : 출력층 활성화 함수의 미분값
        """
        
        # o_error : 손실(Error)
        self.o_error = y - o 
        
        # o_delta : 활성화 함수(시그모이드)의 도함수를 사용하여 출력층 활성화 함수 이전의 미분값
        self.o_delta = self.o_error * self.sigmoidPrime(o)
        
        # z2 error : 은닉층에서의 손실
        self.z2_error = self.o_delta.dot(self.w2.T)
        
        # z2 delta : 활성화 함수(시그모이드)의 도함수를 사용하여 은닉층 활성화 함수 이전의 미분값
        self.z2_delta = self.z2_error*self.sigmoidPrime(self.output_sum)

        # w1, w2를 업데이트
        self.w1 += X.T.dot(self.z2_delta) # X * dE/dY * dY/dy(=Y(1-Y))
        self.w2 += self.activated_hidden.T.dot(self.o_delta) # H1 * Y(1-Y) * (Y - o)
        
    def train(self, X, y):
        """
        실제로 신경망 학습을 진행하는 코드입니다.
        1번의 순전파-역전파, 즉 1 iteration 을 수행하는 함수입니다.
        
        X : 입력 데이터(input)
        y : 타겟값(target value)
        """
        o = self.feed_forward(X)
        self.backward(X,y,o)

수식을 통해 위 코드를 ARABOZA
손실(Error) : $E$
출력층 활성화 함수의 출력값(activated_output) : $A_O$
출력층 활성화 함수의 입력값(=가중합, output_sum) : $S_O$
은닉층 활성화 함수의 출력값(activated_hidden) : $A_H$
은닉층 활성화 함수의 입력값(=가중합, hidden_sum) : $S_H$
$w_2$(=출력층과 은닉층 사이의 가중치) 에 대한 미분

\[\begin{aligned} \frac{\partial E}{\partial w_2} &= \frac{\partial E}{\partial A_O} \cdot \frac{\partial A_O}{\partial w_2}\\ \frac{\partial E}{\partial w_2} &= \frac{\partial E}{\partial A_O} \cdot \frac{\partial A_O}{\partial S_O} \cdot \frac{\partial S_O}{\partial w_2} = \frac{\partial E}{\partial A_O} \cdot \frac{\partial A_O}{\partial S_O} \cdot A_H \quad \bigg( \because A_H = \frac{\partial S_O}{\partial w_2}\bigg) \end{aligned}\]

$w_1$(=은닉층과 입력층 사이의 가중치) 에 대한 미분

\[\begin{aligned} \frac{\partial E}{\partial w_1} &= \frac{\partial E}{\partial A_H} \cdot \frac{\partial A_H}{\partial w_1}\\ \frac{\partial E}{\partial w_2} &= \frac{\partial E}{\partial A_H} \cdot \frac{\partial A_H}{\partial S_H} \cdot \frac{\partial S_H}{\partial w_1} = \frac{\partial E}{\partial A_H} \cdot \frac{\partial A_H}{\partial S_H} \cdot X \quad \bigg( \because X = \frac{\partial S_H}{\partial w_1}\bigg) \end{aligned}\]

역전파 신경망 클래스 학습

# 순전파 후 Error
nn = NeuralNetwork()
nn.train(X,y)
print(nn.o_error)
'''
array([[0.70644301],
       [0.10036169],
       [0.56649547]])
'''

에러(Error, o_error)와 출력층 활성화 함수를 미분한 함수(sigmoidPrime)를 통해서 출력층의 경사(o_delta) 확인
self.o_delta = self.o_error * self.sigmoidPrime(self.output_sum)

# 순전파 시 출력층에서의 가중합을 활성화 함수에 통과
nn.sigmoidPrime(nn.o_error)
'''
array([[0.22123085],
       [0.24937153],
       [0.23096866]])
'''
1000000

# 출력층 활성화 함수 이전의 미분값
# o_delta = o_error * sigmoidPrime(o)
nn.o_delta
'''
array([[0.17285985],
       [0.02468133],
       [0.13902149]])
'''

Hidden Layer Error
이전 단계에서 구했던 출력층의 경사(o_delta)와 출력층의 가중치(w2)를 통해서 은닉층이 받는 손실(z2_error) 계산
self.z2_error = self.o_delta.dot(self.w2.T)

nn.o_delta.dot(nn.w2.T)
'''
array([[-0.28194591, -0.23236088,  0.12295841],
       [-0.04025689, -0.03317703,  0.01755629],
       [-0.22675329, -0.18687483,  0.09888856]])
'''

Hidden Layer Gradient
은닉층 에러(z2_error)와 은닉층 활성화 함수를 미분한 함수(sigmoidPrime)를 통해서 은닉층의 경사(z2_delta)를 계산
self.z2_delta = self.z2_error * self.sigmoidPrime(self.activated_hidden)

nn.activated_hidden
'''
array([[0.43460965, 0.23985861, 0.42340322],
       [0.37111212, 0.48687214, 0.52242758],
       [0.48093658, 0.2520165 , 0.4192448 ]])
'''


nn.z2_delta
'''
array([[-0.06388859, -0.05136035,  0.020324  ],
       [-0.00839476, -0.00674859,  0.00267051],
       [-0.04915074, -0.03951252,  0.01563565]])
'''


X.T.shape == nn.w1.shape
'''
True
'''


nn.z2_delta
'''
array([[-0.06388859, -0.05136035,  0.020324  ],
       [-0.00839476, -0.00674859,  0.00267051],
       [-0.04915074, -0.03951252,  0.01563565]])
'''

Gradient Descent 적용

은닉층 가중치(w1)를 업데이트

`X`에 대해 Transpose 해주는 이유

(필기노트 제공 by Crystal Yim in CS AIB 5th)

X.T
'''
array([[1.   , 0.25 , 0.875],
       [1.   , 0.625, 0.75 ]])
'''


X.T.dot(nn.z2_delta)
'''
array([[-0.10899418, -0.08762095,  0.03467281],
       [-0.10599837, -0.0852126 ,  0.0337198 ]])
'''

출력층 가중치(w2)를 업데이트 합니다.

nn.activated_hidden.T.dot(nn.o_delta)
'''
array([[0.15114662],
       [0.08851428],
       [0.14436766]])
'''

신경망 학습

nn = NeuralNetwork()

# 반복수(epochs or iterations)를 정합니다.
iter = 10000

# 지정한 반복수 만큼 반복합니다.
for i in range(iter):
    if (i+1 in [1,2,3,4,5]) or ((i+1) % 1000 == 0):
        print('+' + '---' * 3 + f'EPOCH {i+1}' + '---'*3 + '+')
        print('입력: \n', X)
        print('타겟출력: \n', y)
        print('예측: \n', str(nn.feed_forward(X)))
        print("에러: \n", str(np.mean(np.square(y - nn.feed_forward(X)))))
    nn.train(X,y)
'''
+---------EPOCH 1---------+
입력: 
 [[1.    1.   ]
 [0.25  0.625]
 [0.875 0.75 ]]
타겟출력: 
 [[1.        ]
 [0.35714286]
 [0.83928571]]
예측: 
 [[0.37768395]
 [0.40886333]
 [0.39684567]]
에러: 
 0.19523515397548788
 '
 '
 '
 +---------EPOCH 10000---------+
입력: 
 [[1.    1.   ]
 [0.25  0.625]
 [0.875 0.75 ]]
타겟출력: 
 [[1.        ]
 [0.35714286]
 [0.83928571]]
예측: 
 [[0.92226356]
 [0.36399293]
 [0.91211178]]
에러: 
 0.0037978381910849734
'''

출력 결과로 반복수가 1-5회일 때의 에러와 이후 1000회 마다의 에러를 볼 수 있다.
점점 에러가 줄어드는 경향성을 확인할 수 있다.

Optimizer

지역 최적점에 빠지게 되는 문제를 방지하기 위한 여러가지 방법 중 하나가 Optimizer
Optimizer: 경사를 내려가는 방법을 결정

Stochastic Gradient Descent

확률적 경사 하강법과 미니 배치(Mini-batch) 경사 하강법
전체 데이터에서 하나의 데이터를 뽑아 신경망에 입력한 후 손실 계산한 후 손실 정보를 역전파하여 신경망의 가중치를 업데이트
장점: 확률적 경사하강법은 1개의 데이터만 사용하여 손실을 계산하기 때문에 가중치를 빠르게 업데이트 할 수 있다.
단점: 1개의 데이터만 보기 때문에 학습 과정에서 불안정한 경사 하강을 보인다.

두 방법을 적당히 융화한 Mini batch Gradient Descent가 등장
N개의 데이터로 미니 배치를 구성하여 해당 미니 배치를 신경망에 입력한 후 이 결과를 바탕으로 가중치 업데이트
일반적으로 미니 배치 경사 하강법을 많이 사용

다양한 Optimizer

SGD
SGD 변형: Momentum, RMSProp, Adam
Newton’s method 등의 2차 최적화 알고리즘 기반 방법: BFGS

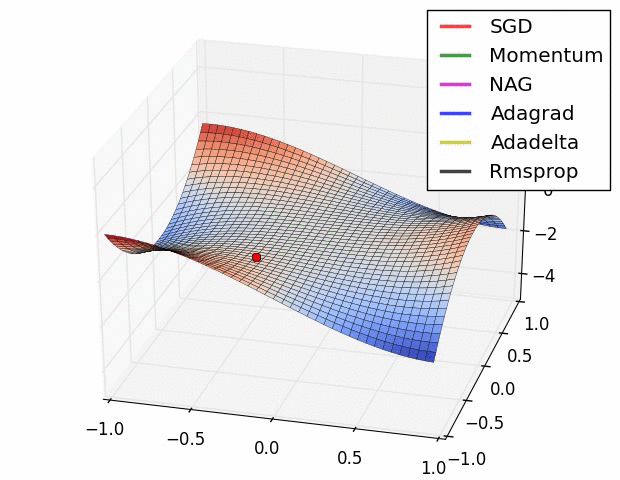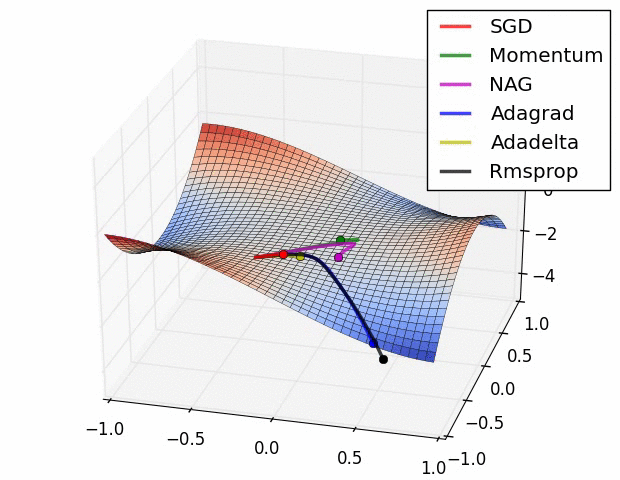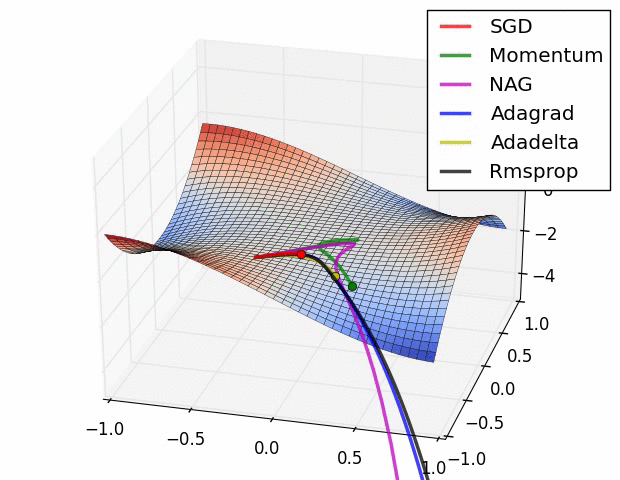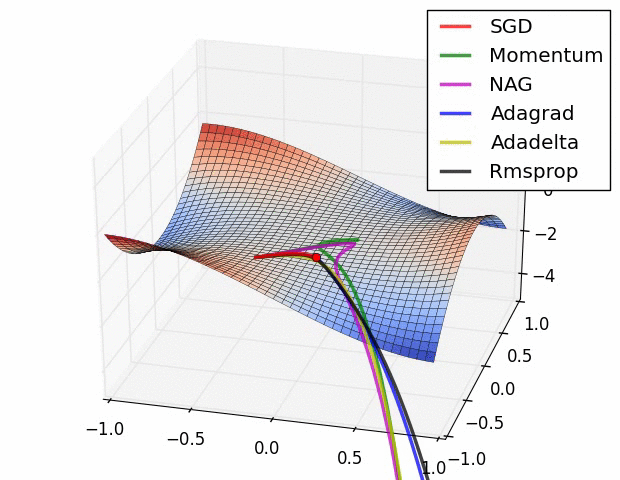
BP Review with Math

오타 수정

$ \partial E_1 \over \partial H_1 $

\[\begin{aligned} \frac{\partial E_1}{\partial H_1} &= \frac{\partial E_1}{\color{blue}{\partial y_1}} \cdot \frac{\color{blue}{\partial y_1}}{\partial H_1} \\ \frac{\partial E_1}{\partial H_1} &= \frac{\partial E_1}{\color{red}{\partial Y_1}} \cdot \frac{\color{red}{\partial Y_1}}{\color{blue}{\partial y_1}} \cdot \frac{\color{blue}{\partial y_1}}{\partial H_1} \end{aligned}\]

$ \partial E_2 \over \partial H_1 $

\[\begin{aligned} \frac{\partial E_2}{\partial H_1} &= \frac{\partial E_2}{\color{green}{\partial y_2}} \cdot \frac{\color{green}{\partial y_2}}{\partial H_1} \\ \frac{\partial E_2}{\partial H_1} &= \frac{\partial E_2}{\color{orange}{\partial Y_2}} \cdot \frac{\color{orange}{\partial Y_2}}{\color{green}{\partial y_2}} \cdot \frac{\color{green}{\partial y_2}}{\partial H_1} \end{aligned}\]

Keras BP 실습

신경망 학습 매커니즘
1. Load data
2. Define model
3. Compile
4. Fit
5. Evaluate

# 앞서 살펴본 선형 데이터를 만들기 위함 함수
def make_samples(n=1000):
    study = np.random.uniform(1, 8, (n, 1))
    sleep = np.random.uniform(1, 8, (n, 1))
    
    y = 5 * study + 2 * sleep + 40
    X = np.append(study, sleep, axis = 1)
    
    # 정규화 
    X = X / np.amax(X, axis = 0)
    y = y / 100
    
    return X, y


import numpy as np
import matplotlib.pyplot as plt
X, y = make_samples()


# Compile
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
 
model = Sequential()

# 신경망 모델 구조 정의
model.add(Dense(3, input_dim=2, activation='sigmoid'))
model.add(Dense(1, activation='sigmoid'))

# 컴파일 단계, 옵티마이저와 손실함수, 측정지표를 연결해서 계산 그래프를 구성을 마무리 합니다.
model.compile(optimizer='sgd', loss='mse', metrics=['mae', 'mse'])
# model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy']) # 분류인 경우 예시

results = model.fit(X,y, epochs=50)
'''
Epoch 1/50
32/32 [==============================] - 1s 1ms/step - loss: 0.0819 - mae: 0.2704 - mse: 0.0819
Epoch 2/50
32/32 [==============================] - 0s 987us/step - loss: 0.0738 - mae: 0.2550 - mse: 0.0738
Epoch 3/50
32/32 [==============================] - 0s 1ms/step - loss: 0.0665 - mae: 0.2402 - mse: 0.0665
'
'
'
Epoch 48/50
32/32 [==============================] - 0s 1ms/step - loss: 0.0100 - mae: 0.0835 - mse: 0.0100
Epoch 49/50
32/32 [==============================] - 0s 998us/step - loss: 0.0099 - mae: 0.0834 - mse: 0.0099
Epoch 50/50
32/32 [==============================] - 0s 1ms/step - loss: 0.0099 - mae: 0.0832 - mse: 0.0099
'''


results.history.keys()
'''
dict_keys(['loss', 'mae', 'mse'])
'''


# visualization
plt.plot(results.history['loss'])
plt.plot(results.history['mae'])

Fashin MNIST

from tensorflow.keras.datasets import fashion_mnist

# 데이터 불러오기
(X_train, y_train), (X_test, y_test) = fashion_mnist.load_data()


# 데이터를 정규화 합니다
X_train = X_train / 255.
X_test = X_test /255.


import matplotlib.pyplot as plt

for i in range(9):
    # subplot 정의
    plt.subplot(3, 3, i+1)
    
    # 데이터를 plot 합니다.
    plt.imshow(X_train[i], cmap=plt.get_cmap('gray'))
    plt.axis('off')
    
plt.show()

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten


model = Sequential() 
model.add(Flatten(input_shape=(28, 28))) # 28*28 = 784 특성 벡터로 펼쳐 변환해 Dense 층으로 들어갑니다
model.add(Dense(10, activation='softmax'))

model.compile(optimizer='adam'
             , loss='sparse_categorical_crossentropy'
             , metrics=['accuracy'])

model.summary()
'''
Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
flatten (Flatten)            (None, 784)               0         
_________________________________________________________________
dense_2 (Dense)              (None, 10)                7850      
=================================================================
Total params: 7,850
Trainable params: 7,850
Non-trainable params: 0
_________________________________________________________________
'''


# 모델 학습
model.fit(X_train, y_train, epochs=10, validation_data=(X_test,y_test))
# model.fit(X_train, y_train, epochs=5)
'''
Epoch 1/10
1875/1875 [==============================] - 3s 2ms/step - loss: 0.6010 - accuracy: 0.7971 - val_loss: 0.5208 - val_accuracy: 0.8167
Epoch 2/10
1875/1875 [==============================] - 3s 1ms/step - loss: 0.4616 - accuracy: 0.8427 - val_loss: 0.4759 - val_accuracy: 0.8338
Epoch 3/10
1875/1875 [==============================] - 3s 1ms/step - loss: 0.4355 - accuracy: 0.8510 - val_loss: 0.4702 - val_accuracy: 0.8347
Epoch 4/10
1875/1875 [==============================] - 3s 1ms/step - loss: 0.4223 - accuracy: 0.8538 - val_loss: 0.4745 - val_accuracy: 0.8318
Epoch 5/10
1875/1875 [==============================] - 3s 1ms/step - loss: 0.4153 - accuracy: 0.8570 - val_loss: 0.4580 - val_accuracy: 0.8383
Epoch 6/10
1875/1875 [==============================] - 3s 1ms/step - loss: 0.4072 - accuracy: 0.8599 - val_loss: 0.4736 - val_accuracy: 0.8383
Epoch 7/10
1875/1875 [==============================] - 3s 1ms/step - loss: 0.4035 - accuracy: 0.8599 - val_loss: 0.4466 - val_accuracy: 0.8481
Epoch 8/10
1875/1875 [==============================] - 2s 1ms/step - loss: 0.3974 - accuracy: 0.8624 - val_loss: 0.4552 - val_accuracy: 0.8424
Epoch 9/10
1875/1875 [==============================] - 3s 1ms/step - loss: 0.3945 - accuracy: 0.8635 - val_loss: 0.4425 - val_accuracy: 0.8454
Epoch 10/10
1875/1875 [==============================] - 3s 1ms/step - loss: 0.3930 - accuracy: 0.8635 - val_loss: 0.4513 - val_accuracy: 0.8429
<keras.callbacks.History at 0x7f9266bda550>
'''


# 예측
model.predict(X_test[0:1])
'''
array([[5.62648438e-07, 1.74089614e-08, 1.51180375e-05, 3.10818064e-06,
        4.04791763e-06, 5.53222373e-02, 3.58409670e-05, 3.93314958e-02,
        6.38620043e-03, 8.98901403e-01]], dtype=float32)
'''


# 정확도
test_loss, test_acc = model.evaluate(X_test,  y_test, verbose=2)
'''
313/313 - 0s - loss: 0.4513 - accuracy: 0.8429
'''

Review

신경망(Neural Network)에서 사용할 초기 가중치(파라미터,parameter)를 임의 설정
설정한 파라미터를 이용하여 입력 데이터를 신경망에 넣은 후 순전파 과정을 거쳐 출력값(Output)을 수신
출력값과 타겟(Target, Label)을 비교하여 손실(Loss) 계산
손실(Loss)의 Gradient를 계산하여 Gradient가 줄어드는 방향으로 가중치 업데이트합니다.
이 때 각 가중치의 Gradient를 계산할 수 있도록 손실 정보를 전달하는 과정이 역전파(Backpropagation)
얼마만큼의 데이터를 사용하여 가중치를 어떻게 업데이트 할 지 결정
이를 옵티마이저(Optimizer)라는 하이퍼파라미터로 선정(Stochastic or Batch 등)

[Deep Learning] Gradient Decent & Backpropagation

신경망 구조(recap.)

신경망 학습 알고리즘 요약

Cost Func or Loss Func

Backpropagation

Exemple

분석

HOW?

Convex/Concave func과 Local Optima

Update weight: BP

역전파 신경망 클래스 학습

Gradient Descent 적용

`X`에 대해 Transpose 해주는 이유

신경망 학습

Optimizer

Stochastic Gradient Descent

다양한 Optimizer

BP Review with Math

Keras BP 실습

Fashin MNIST

Review

References

신경망 구조(recap.)

신경망 학습 알고리즘 요약

Cost Func or Loss Func

Backpropagation

Exemple

분석

HOW?

Convex/Concave func과 Local Optima

Update weight: BP

역전파 신경망 클래스 학습

Gradient Descent 적용

X에 대해 Transpose 해주는 이유

신경망 학습

Optimizer

Stochastic Gradient Descent

다양한 Optimizer

BP Review with Math

Keras BP 실습

Fashin MNIST

Review

References

`X`에 대해 Transpose 해주는 이유