퍼셉트론(Perceptron)과 인공신경망(Artificial Neural Networks)
- 퍼셉트론(Perceptron), 가중치(Weight), 입력(Input)과 출력(Output)
역전파(Backpropagation)
- 경사 하강법(Gradient Descent), 학습률(Learning rate)
과적합(Overfitting)을 막기 위한 방법
- 가중치 감소/제한(Weight Decay/Constraint), Dropout, 조기 종료(Early Stopping)
신경망 하이퍼파라미터(Hyperparameter) 튜닝, 실험 추적 시스템
- Keras tuner, wandb

2주차

텍스트 전처리(Text Preprocessing)와 횟수 기반의 벡터화
- 불용어, 어간 추출(Stemming)과 표제어 추출(Lemmatization), BoW, TF-IDF
분산 기반의 벡터화와 임베딩(Embedding)
- 임베딩(Embedding), Word2Vec, OOV, fastText
언어 모델과 순환 신경망(RNN)
- 언어 모델(Language Model), RNN, LSTM, GRU, Attention
트랜스포머(Transformer)와 그 이후
- Transformer, Self-Attention, 사전 학습된 언어 모델, GPT, BERT

3주차

합성곱 신경망(CNN)과 이미지 처리
- Convolution, Pooling, Transfer Learning
구분(Segmenatation)과 객체 탐지(Object Detection)
- FCN, Unet, RCNN, YOLO
오토인코더(AutoEncoder)
- Latent Vector, 이상치 탐지(Anomaly Detection)
GAN(Generative Adversarial Network)
- Generator vs Discriminator, DCGAN, CycleGAN

전문용어 없이 듣는 딥러닝의 모든 것

바로가기
1943년: Warren McCulloch
- 기계학습 = 사람학습
- 신경망 연구
1958년: Frank Rosenblatt
- 기존 신경망 모델을 발전
- 응용을 활용하여 실제 문제 해결
XOR 문제(배타적 논리합): 퍼셉트론은 나쁜 학습법 - 민스키

1980: MLP(Multi Layer Perceptron)

1986: 역전파법

AI의 역사

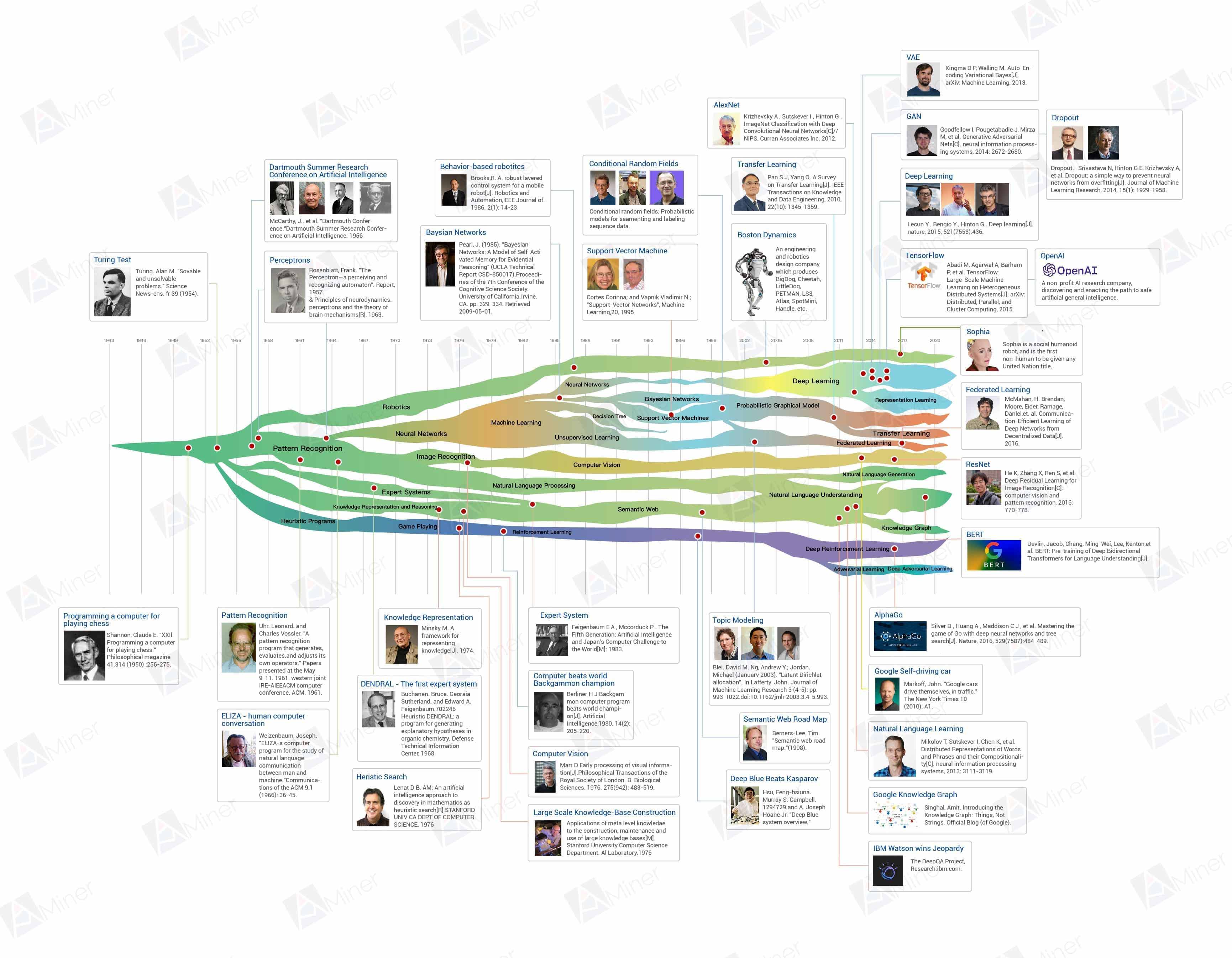
패턴 인식(Pattern Recognition)
- 신경망(Neural Networks)
  - 머신러닝(Machine Learning)
  - 딥러닝(Deep Learning)
- 이미지 인식(Image Recogition)
  - 컴퓨터 비전(Computer Vision) → 딥러닝 기반 컴퓨터 비전
- 자연어 처리(Natural Language Processing) → 딥러닝 기반 자연어처리
  - 자연어 이해(Natural Language Understanding)
  - 자연어 생성(Natural Language Generation)
휴리스틱 프로그램(Heuristic Programs)
- 게임 기술(Game Playing)
  - 강화학습(Reinforcement Learning) → 딥러닝 기반 강화학습
로보틱스(Robotics)

Why Deep Learning?

1950년 처음 제시된 신경망 아이디어는 많은 주목을 받지 못했다.
MLP의 발전 등으로 강력한 기술이 되었다.
Object Detection, Segmentation, NLP 등 기존 머신러닝 알고리즘이 잘 못 풀던 영역에서도 사람보다 뛰어난 성과를 보인다.

발전 이유

핵심 알고리즘의 발전
딥러닝 프레임워크(Framework)의 발전 : Tensorflow, Keras, PyTorch 등
GPU의 발전으로 인한 계산 속도 증가 : CUDA 와 같은 라이브러리 등장
벤치마크 데이터셋(Dataset) 등 기반이 되는 데이터셋 마련 : ImageNet, GLUE

How

신경망에 대한 거부감 없애기
새로운 개념을 글로 적거나, 말해보면서 제대로 알고 있는지 확인

Perceptron

뉴런을 모사하여 만들어진 신경망을 이루는 가장 기본 단위

프랑크 로젠블라트(Frank Rosenblatt)가 1957년 고안
퍼셉트론이 신경망(딥러닝)의 기원이 되는 알고리즘
다수의 신호를 입력으로 받아 하나의 신호를 출력
- 신호: 전류와 같은 일종의 흐름
- 퍼셉트론은 입력 데이터와 가중치가 연산의 흐름을 만들어 정보를 계속해서 전달
- 가중치는 전류에서 말하는 저항에 해당
- 저항이 낮을수록 큰 전류가 흐르지만, 반대로 퍼셉트론에서는 가중치가 클수록 강한 신호를 흘려보낸다.
Perceptron = Perception + Neuron
- Perception : 무언가를 인지하는 능력
- Neuron : 감각 입력 정보를 의미있는 정보로 바꿔주는 뇌에 있는 신경 세포
뉴런이 감각 정보를 받아서 문제를 해결하는 원리를 따라한 인공 뉴런으로써 입력 값에 대해 가중치를 적용해 계산한 후, 확인해서 결과를 전달한다.
퍼셉트론은 자신이 내린 결과를 확인해서, 미래에는 더 나은 결정을 하도록 자기 자신을 수정한다.
하나의 뉴런만으로 아무것도 할 수 없음. 퍼셉트론도 마찬가지
하나의 노드(뉴런)으로 이루어진 신경망의 기본 구조이며, 다수의 입력값을 받아 하나의 출력값을 내보낸다.

노드는 입력값에 가중치(와 편향)가 곱해진 값을 모두 더하는 연산, 즉 선형 결합을 하고 활성화 함수를 적용한 후 그 값을 출력
- Bias(편향): 해당 Perceptron이 얼마나 쉽게 활성화 되는지를 조절하는 매개변수

수식

$f$는 활성화 함수
먼저 가중치와 편향을 입력 신호와 연산한 값을 더한$\big(\sum\big)$ 뒤에, 활성화 함수$(f)$에 넣어준다.

$y = f \bigg[\sum(b + w_0x_0 + w_1x_1 + … + w_nx_n) \bigg]$

만약 활성화 함수가 위에서 구현했던 계단 함수라면

$ f(\mathbf {x} )={\begin{cases}1&{\text{if }}\ \mathbf {w} \cdot \mathbf {x} +b>0, \ 0&{\text{otherwise}}\end{cases}} $

Logic Gate

AND GATE

입력 신호가 모두 1(True)일 때 1(True)을 출력

# w1, w2는 가중치(weight)

def AND(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7
    tmp = x1*w1 + x2*w2
    
    if tmp <= theta:
        return 0
    else:
        return 1

print(AND(0, 0))
print(AND(1, 0))
print(AND(0, 1))
print(AND(1, 1))
'''
0
0
0
1
'''

NAND GATE

Not AND 의 줄임말로 AND GATE의 결과의 반대를 출력

def NAND(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7
    tmp = x1*w1 + x2*w2
  
    if tmp <= theta:
        return 1
    else:
        return 0

print(NAND(0, 0))
print(NAND(1, 0))
print(NAND(0, 1))
print(NAND(1, 1))
'''
1
1
1
0
'''

OR GATE

입력 신호 중 하나만 1(True)이라도 1(True)을 출력

def OR(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.3
    tmp = x1*w1 + x2*w2
  
    if tmp <= theta:
        return 0 
    else:
        return 1

print(OR(0, 0))
print(OR(1, 0))
print(OR(0, 1))
print(OR(1, 1))
'''
0
1
1
1
'''

XOR GATE

배타적 논리합(Exclusive-OR)이라고도 불리는 GATE. 입력 신호가 다를 경우 1(True)을 출력

신경망이 논의되던 초기에 퍼셉트론의 한계로 지적되었던 것이 바로 XOR GATE 의 표현

여러 개의 선을 아무리 그어보아도 하나의 직선으로는 흰점과 검은점을 구분할 수 없다.

XOR 문제

퍼셉트론의 한계를 설명할 때 등장하는 XOR(exclusive OR) 문제
XOR 문제는 논리 회로에 등장하는 개념
컴퓨터는 두 가지의 디지털 값, 즉 0과 1을 입력해 하나의 값을 출력하는 회로가 모여 만들어지는데, 이 회로가 ‘게이트(gate)’

AND와 OR 게이트는 직선을 그어 결괏값이 1인 값(검은점)을 구별할 수 있다.
그러나 XOR의 경우 선을 그어 구분할 수 없다.
이는 인공지능 분야의 선구자였던 MIT의 마빈 민스키(Marvin Minsky) 교수가 1969년에 발표한 <퍼셉트론즈(Perceptrons)>라는 논문에 나오는 내용
‘뉴런 → 신경망 → 지능’이라는 도식을 따라 ‘퍼셉트론 → 인공 신경망 → 인공지능’이 가능하리라 꿈꾸던 당시 사람들은 이것이 생각처럼 쉽지 않다는 사실을 깨닫게 된다.
알고 보니 간단한 XOR 문제조차 해결할 수 없었던 것
이 논문 이후 인공지능 연구가 한동안 침체기를 겪게 된다.
10여 년이 지난 후에야 이 문제가 해결되는데, 이를 해결한 개념이 바로 다층 퍼셉트론(multilayer perceptron)
XOR 문제의 해결은 평면을 휘어주는 것!
XOR 문제를 해결하기 위해서 두 개의 퍼셉트론을 한 번에 계산할 수 있어야 한다.
이를 가능하게 하는 숨어있는 층이 은닉층(hidden layer)

신경망

1943년경 뇌의 신경 활동을 수학으로 표현하고자 한 아이디어와 1957년에 로젠블라트(Rosenblatt)가 고안한 퍼셉트론이 발전
ANN(Artificial Neural Networks), 즉 인공 신경망은 실제 신경계의 특징을 모사하여 만들어진 계산 모델
인공 신경망의 기본 구조인 퍼셉트론은 실제 뇌 신경망의 기본 구조인 뉴런(Neuron)을 모사하여 제작
뉴럴넷(Neural-Net)

신경망의 기본 형태(가중치, 편향 연산)

원으로 표현된 부분을 뉴런(Neuron) 혹은 노드(node)
1. 입력 신호($x_0, x_1, …$)가 입력되면 각각 고유한 가중치($w_0, w_1, …$)가 곱해진다.
2. 다음 노드에서는 입력된 모든 신호를 더해준다.($\sum$).
3. 각 노드에서의 연산값이 정해진 임계값(Threshold Logic Unit)을 넘을 경우에만 다음 노드들이 있는 층(layer)으로 신호를 전달한다.
목표: 복잡한 데이터 속에서 패턴을 발견할 수 있는 알고리즘으로서의 인공 신경망을 만드는 것

Activation Func

활성화 함수는 인공지능의 많은 알고리즘에서 다양한 형태로 사용된다.
어떠한 활성화 함수를 사용하느냐에 따라 그 출력 값이 달라지기 때문에, 적절한 활성화 함수를 사용하는 것은 중요하다.
활성화 함수: 어떠한 신호를 입력받아 이를 적절한 처리를 하여 출력해주는 함수
각 노드에서의 연산값이 정해진 임계값을 넘을 경우에만 다음 노드들이 있는 층으로 신호를 전달
신경망에서 각 노드는 활성화 함수를 갖고 있다.
각 층에는 같은 종류의 활성화 함수를 사용한다.
인공신경망에서 활성화 함수는 다음 층으로 신호를 얼마만큼 전달할지 결정한다.
그래서 간혹 Transfer func(전달함수)라고 부른다.

가장 간단한 활성화 함수인 3개(Step, Sigmoid, ReLU)
활성화 함수는 신경망의 output을 결정하는 식
각 뉴런은 가중치를 가지며 이것은 input number와 곱해져 다음 레어로 전달
이 때 활성화 함수는 현재 뉴런의 input을 feeding하여 생성된 output이 다음 레이어로 전해지는 과정 중 역할을 수행하는 수학적인 게이트

Step func

입력 값이 임계값을 넘기면 1을 출력하고, 그렇지 않으면 0을 출력하는 함수

import numpy as np
import matplotlib.pyplot as plt 
import math 

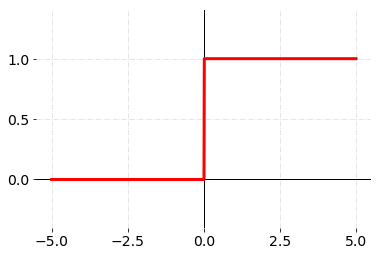
x = np.array([-1, 1, 2])
print("input : ", x)

y = x>0
print("Logic : ", y)

y = y.astype(np.int)
print("Boolean : ", y)
'''
input :  [-1  1  2]
Logic :  [False  True  True]
Boolean :  [0 1 1]
'''

def step_function(x):
  return np.array(x>0, dtype=np.int)

print(step_function(-1))
print(step_function(0.5))
print(step_function(500000))
'''
0
1
1
'''

x = np.linspace(-1, 1, 100)
plt.step(x, step_function(x)) 
plt.show()

Sigmoid func

신경망이 경사 하강법을 통해 학습을 진행하기 위해서는 ‘미분’과정이 필요한데 Sigmoid가 해결해준다.

def sigmoid(x):
  return 1/ (1+np.exp(-x))

x = np.array([-5, -1, 0, 0.1, 5, 500000])
print(sigmoid(x))
'''
[0.00669285 0.26894142 0.5        0.52497919 0.99330715 1.        ]
'''

x = np.linspace(-10, 10, 100) 
  
plt.plot(x, sigmoid(x)) 
plt.xlabel("x") 
plt.ylabel("Sigmoid(X)") 
  
plt.show() 

ReLU func

많이 사용되는 활성화 함수

def ReLU(x):
    zero = np.zeros(len(x))
    return np.max([zero, x], axis=0)

x = np.arange(-3, 3, .1)
y = ReLU(x)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, y)
ax.set_ylim([-1.0, 3.0])
ax.set_xlim([-3.0, 3.0])
#ax.grid(True)
ax.set_xlabel('z')
ax.set_title('ReLU: Rectified linear unit')

plt.show()
fig = plt.gcf()

구현

초기 상태 설정

가중치와 편향의 값은 임의로 지정

# 네트워크 구조 생성 함수 정의
def init_network():
    """
    W1,W2 : 가중치
    B1,B2 : 편향
    """
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5, 0.7],
                            [0.1, 0.3, 0.3, 0.7],
                            [0.2, 0.1, 0.6, 0.8]]) # 3 x 4
    network['B1'] = np.array([0.11, 0.12, 0.13, 0.14])
    network['W2'] = np.array([[0.1, 0.5],
                            [0.2, 0.6],
                            [0.3, 0.4],
                            [0.35, 0.35]]) # 4 x 2
    network['B2'] = np.array([0.1, 0.5])

    return network

순전파 함수 정의

순전파(Forward Propagation): 가중치와 편향의 연산을 반복하며 입력값을 받아 출력값으로 반환하는 과정
딥러닝에서 입력 데이터가 있으면 신경망을 따라서 쭉 신호를 전파해서(가중치와 편향의 연산 반복) 최종 출력을 만들어가는 과정

# 순전파 함수 정의
def forward(network, x):
  W1, W2 = network['W1'], network['W2']
  b1, b2 = network['B1'], network['B2']

  a1 = np.dot(x, W1) + b1
  z1 = sigmoid(a1)
  a2 = np.dot(z1, W2) + b2
  
  y = a2
  return y

계산한 값 출력

# 네트워크 제작
network = init_network()

# 샘플 입력 데이터
x = np.array([1, 0.5, 0.7])

# 순전파 실행
y = forward(network, x)
print(y)
'''
[0.81956037 1.7977893 ]
'''

위 코드는 학습없이 단순히 입력 값에 가중치를 연산하여 출력을 내는, 즉 한 번의 순전파가 일어나는 간단한 신경망

가중치 행렬과 입력 신호의 연산

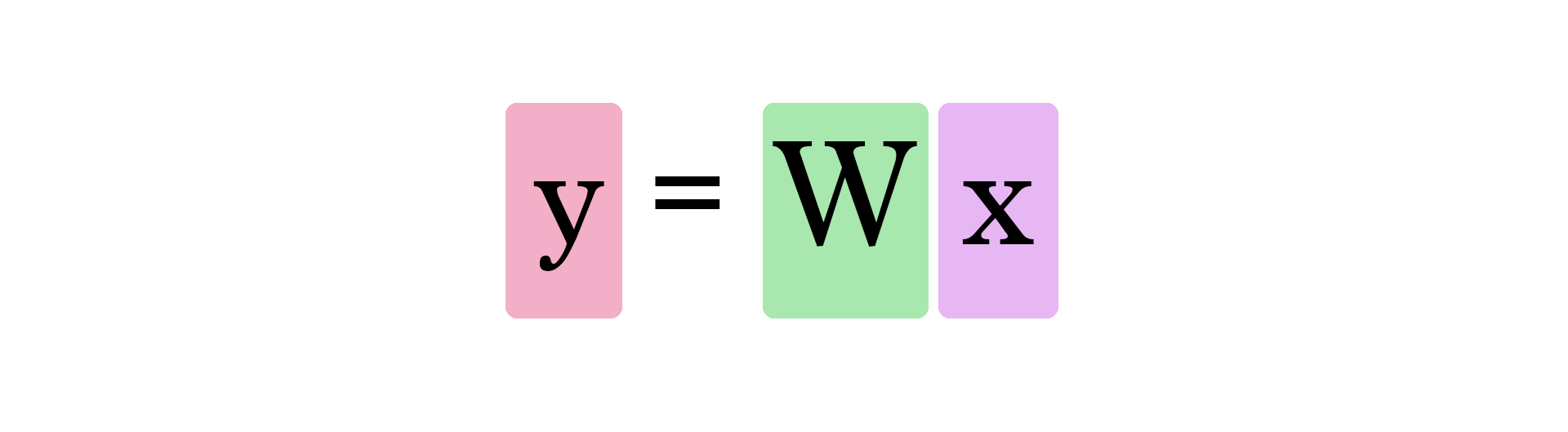
신경망은 노드가 가중치로 연결되어 입력 신호와 연산한 뒤에 출력값으로 내보내는 함수라고도 할 수 있다.
가중치를 지속하여 수정하면서 적절한 가중치를 찾는 과정을 학습(Training, Learning)이라고 한다.

여러가지 신경망 구조

THE NEURAL NETWORK ZOO

Layer

Input Layer

데이터셋이 입력되는 층
입력되는 데이터셋의 특성(Feature)에 따라 입력층 노드의 수가 결정
보통 입력층은 어떤 계산도 수행하지 않고 그냥 값들을 전달하기만 하는 특징을 가지고 있다.
그렇기 때문에 신경망의 층수(깊이, depth)를 셀 때 입력층은 포함하지 않는다.

Hidden Layer

입력층으로부터 입력된 신호가 가중치, 편향과 연산되는 층
일반적으로 입력층과 출력층 사이에 있는 층을 은닉층이라고 부른다.
은닉층에서 일어나는 계산의 결과를 사용자가 볼 수 없기 때문에 ‘은닉(Hidden)층’ 이라는 이름이 붙었다.
은닉층은 입력 데이터셋의 특성 수와 상관 없이 노드 수를 구성할 수 있다.
일반적으로 딥러닝(Deep Learning)이라고 하면 2개 이상의 은닉층을 가진 신경망
은닉층의 수가 늘어나고 더 좋은 학습 방법이 개발되면서 복잡한 데이터의 구조를 학습할 수 있게 되었다.
이렇게 복잡한 신경망이 다른 알고리즘이 세웠던 성능을 갱신하면서 딥러닝이 유명해졌다.

Output Layer

가장 마지막에 위치한 층이며 은닉층 연산을 마친 값이 출력되는 층
문제 종류에 따라서 출력층을 잘 설계하는 것이 중요하다.

이진 분류(Binary Classification)

활성화 함수로는 시그모이드(Sigmoid) 함수를 사용하며 출력층의 노드 수는 1로 설정
출력되는 값이 0과 1 사이의 확률값

다중 분류(Multi-class Classification)

활성화 함수로는 소프트맥스(Softmax) 함수를 사용하며 출력층의 노드 수는 레이블의 클래스(Class) 수와 동일하게 설정

회귀(Regression)

일반적으로는 활성화 함수를 지정해주지 않으며 출력층의 노드 수는 출력값의 특성(Feature) 수와 동일하게 설정(항등 함수)
단순히 하나의 수를 예측하는 문제라면 1

TF Exemple

MNIST

import pandas as pd
import tensorflow as tf


# import
mnist = tf.keras.datasets.mnist

# Training Set, Test Set을 분류
(x_train, y_train), (x_test, y_test) = mnist.load_data()

# Value normalization
x_train, x_test = x_train / 255.0, x_test / 255.0


# 처음보는 데이터의 경우 데이터 자체를 디스플레이 하여 보면 도움이 됩니다.
pd.unique(y_train)
'''
array([5, 0, 4, 1, 9, 2, 3, 6, 7, 8], dtype=uint8)
'''


# 신경망 모델 구축
model = tf.keras.models.Sequential([
  tf.keras.layers.Flatten(input_shape=(28, 28)),
  tf.keras.layers.Dense(100, activation='relu'),
  tf.keras.layers.Dropout(0.2), # 과적합(Overfitting)을 방지
  tf.keras.layers.Dense(10, activation='softmax')
])


# 구축한 모델을 컴파일하며, 옵티마이저, loss function 등을 설정
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])


# 모델이 학습을 하는 부분
model.fit(x_train, y_train, epochs=5) # epoch의 수를 변화시키면 더 많이 학습하거나 적게 학습
'''
Train on 60000 samples
Epoch 1/5
WARNING:tensorflow:Entity <function Function._initialize_uninitialized_variables.<locals>.initialize_variables at 0x7f9aa9267b00> could not be transformed and will be executed as-is. Please report this to the AutoGraph team. When filing the bug, set the verbosity to 10 (on Linux, `export AUTOGRAPH_VERBOSITY=10`) and attach the full output. Cause: module 'gast' has no attribute 'Index'
WARNING: Entity <function Function._initialize_uninitialized_variables.<locals>.initialize_variables at 0x7f9aa9267b00> could not be transformed and will be executed as-is. Please report this to the AutoGraph team. When filing the bug, set the verbosity to 10 (on Linux, `export AUTOGRAPH_VERBOSITY=10`) and attach the full output. Cause: module 'gast' has no attribute 'Index'
60000/60000 [==============================] - 5s 91us/sample - loss: 0.3148 - accuracy: 0.9090
Epoch 2/5
60000/60000 [==============================] - 5s 80us/sample - loss: 0.1581 - accuracy: 0.9538
Epoch 3/5
60000/60000 [==============================] - 5s 79us/sample - loss: 0.1230 - accuracy: 0.9633
Epoch 4/5
60000/60000 [==============================] - 5s 80us/sample - loss: 0.1016 - accuracy: 0.9692
Epoch 5/5
60000/60000 [==============================] - 5s 80us/sample - loss: 0.0862 - accuracy: 0.9743
<tensorflow.python.keras.callbacks.History at 0x7f9aa926ec10>
'''


# 만들어진 모델을 이용하여 예측
model.evaluate(x_test,  y_test, verbose=2)
'''
10000/1 - 0s - loss: 0.0420 - accuracy: 0.9755
[0.08292745780413971, 0.9755]
'''

텐서플로우 플레이그라운드
❓ Flatten 역할
❓ 마지막 Dense 층의 숫자 10
❓ 마지막 Dense 층의 activation softmax
❓ compile 이 있는 부분에서 loss 함수

Why Powerful?

깊은 신경망, 즉 딥러닝은 복잡한 데이터셋에서도 패턴을 잘 찾아내어 분류, 회귀 등의 문제를 뛰어난 성능으로 풀어낸다.
이미지, 텍스트 데이터와 같이 차원이 많고 복잡한 데이터에서 패턴을 찾으려면, 매우 복잡한 특성 조합이 필요하다.

Representation Learning(표현학습)

머신러닝을 수행할 때에는 직접 데이터셋이 가진 특성(Feature)을 최대한 파악한 후 가장 중요한 특성만을 설계하고 찾아내야 했다.
그 과정이 Feature Engineering을 바탕으로 한 전처리
전처리 이후에 머신러닝 모델에 넣어주어야 모델의 성능을 올릴 수 있었고 전처리를 생략한다면 성능이 잘 나오지 않았다.
반면에 신경망은 데이터에서 필요한 특성을 알아서 조합하여 찾아낸다.
최소한의 전처리만 해준 후에 모델에 넣어도 꽤 성능이 잘 나오게 된다. 즉, 심화된 특성 공학을 사용해 특성 간의 관계를 찾아낼 필요가 없다.
스스로 특성 관계를 찾아내는 것을 표현 학습(Representation learning)

❓ 그렇다면 신경망의 구조를 어떻게 설계하는 것이 가장 좋을까? 좋은 신경망 구조란 무엇일지 각자 생각해보자

Neural Network in Python

# 입력 데이터 생성
np.random.seed(405)

# X: 입력(inputs)
X = np.array([
    [0, 0]
    ,[0, 1]
    ,[1, 0]
    ,[1, 1]
])

# 편향(bias)
b = 1

# Y: 타겟값(target, correct outputs)
Y= np.array([[0],[1],[1],[1]])


# 활성화 함수인 시그모이드(Sigmoid) 함수와 그 도함수를 구현
# 시그모이드 함수
# net: 입력과 가중치의 가중합
def sigmoid(net):
    return 1 / (1 + np.exp(-net))

# 시그모이드 함수의 도함수 유도 예시
# https://towardsdatascience.com/derivative-of-the-sigmoid-function-536880cf918e
def sigmoid_prime(net):
    sig = sigmoid(net)
    return sig * (1 - sig)


# 시그모이드 함수가 잘 생성되었는지 그래프 출력
x_range = np.arange(-10., 10., 0.2)
y_range = np.array([sigmoid(x) for x in x_range])
y_prime = np.array([sigmoid_prime(x) for x in x_range])

plt.plot(x_range, y_range, label='sigmoid') 
plt.plot(x_range, y_prime, label='sigmoid_prime')
plt.legend()
plt.show();

# 초기 가중치는 무작위(Random)로 지정
# W: [w0, w1]
W = 2 * np.random.rand(2,1) - 1
W
'''
array([[ 0.40316676],
       [-0.44345216]])
'''


# 입력 데이터와 가중치 연산
# Z: 신호에 가중치와 편향을 연산해 준 결과
Z = np.dot(X, W) + b
Z
'''
array([[1.        ],
       [0.55654784],
       [1.40316676],
       [0.9597146 ]])
'''


# 활성화 함수를 적용한 뒤 나오는 값(output)을 출력
# A: 출력(activated outputs)
A = sigmoid(Z)
A
'''
array([[0.73105858],
       [0.6356534 ],
       [0.80268592],
       [0.72306466]])
'''

backpropagation(역전파)

출력 오차를 줄이기 위한 경사 하강법 이용
손실(error, cost)을 계산하기 위해 실제 타겟값(target)과 출력값(output)의 차이를 계산
경사 하강법(Gradient descent): 손실 값이 최소가 되는 가중치(weight)를 찾는 방법
역전파 알고리즘은 경사 하강법에 필요한 미분값을 빠르고 효율적으로 찾는 알고리즘

MSE 미분

손실 함수(Cost function)로 MSE(Mean Squared Error)를 사용할 때,
가중치에 대해 도함수를 아래와 같은 수식으로 나타낼 수 있다. 참조 링크

\[\frac{\partial E}{\partial w_j} = \frac{\partial}{\partial w_j} \frac{1}{2n} \sum_{i=1}^{n} (t_i - o_i)^2\] \[= \frac{1}{2n} \sum_{i=1}^{n} \frac{\partial}{\partial w_j} (t_i - o_i)^2 \quad [\text{chain rule}]\] \[= \frac{1}{2n} \sum_{i=1}^{n} 2 (t_i - o_i) \frac{\partial}{\partial w_j} (t_i - o_i) \quad [\text{sum rule}]\] \[= \frac{1}{n} \sum_{i=1}^{n} (t_i - o_i) \left( \frac{\partial}{\partial w_j} t_i - \frac{\partial}{\partial w_j} o_i \right)\] \[= - \frac{1}{n} \sum_{i=1}^{n} (t_i - o_i) \frac{\partial}{\partial w_j} o_i.\]

와 같은 형태가 되고 $o_i$ 를 $w_j$에 관해 편미분 하면

\[\frac{\partial}{\partial w_j} o_i\] \[= \frac{\partial o_i}{\partial \text{net}_i}\frac{\partial\text{net}_i}{\partial {w_j}}\]

라고 쓸 수 있다. 벡터 계산 코드로 구현하면 다음과 같고 이를 가중치 업데이트에 사용한다.

da = $\partial E/\partial A$ (MSE를 미분하여 나오는 값)
dz = $\partial E/\partial z$
dw, db = 각각 가중치(weight), 편향(bias) 업데이트 값

# 미분 값 코드 구현
da = A - Y
dz = da * sigmoid_prime(Z)
dw = np.dot(X.T, dz)
db = np.sum(da, keepdims=True)

print("dz : \n", dz, "\n")
print("dw : \n", dw, "\n")
print("db : \n", db, "\n")
'''
dz : 
 [[ 0.14373484]
 [-0.084382  ]
 [-0.03125085]
 [-0.05545413]] 

dw : 
 [[-0.08670498]
 [-0.13983613]] 

db : 
 [[-0.10753744]] 
'''


print("기존 가중치: \n", W, "\n")
'''
기존 가중치: 
 [[ 0.40316676]
 [-0.44345216]] 
'''


# 가중치와 편향 업데이트
# 가중치 업데이트(batch)
W += dw
b += db
print("업데이트 후 가중치: \n", W, "\n")
print("업데이트 후 bias: \n", b, "\n")
'''
업데이트 후 가중치: 
 [[ 0.31646178]
 [-0.58328829]] 

업데이트 후 bias: 
 [[0.89246256]] 
'''


# 반복하여 최적의 가중치를 찾기
# 이미 입력 데이터와 타겟 출력은 윗 부분에서 선언

# 가중치 초기화
# W = 2 * np.random.random((2,1)) - 1
W = np.random.randn(2,1)
# W = np.zeros((2,1))

b = 0

print('학습 전 가중치: \n', W)

# 가중치 업데이트를 10,000회 (10,000 epoch) 진행

for iteration in range(1000):

    # 순방향 전파
    Z = np.dot(X, W) + b
    A = sigmoid(Z)

    # 역방향 전파(기울기 계산)
    da = Y - A
    dz = da * sigmoid_prime(Z)
    dw = np.dot(X.T, dz)
    db = np.sum(da, keepdims=True)
    
    W += dw
    b += db

print('학습 후 가중치: \n', W, "\n")
print('학습 후 bias: \n', b, "\n")
print('학습 후 예측값: \n', A.round(3), "\n")
'''
학습 전 가중치: 
 [[-0.79003947]
 [ 0.6826574 ]]
학습 후 가중치: 
 [[5.92060487]
 [5.92082351]] 

학습 후 bias: 
 [[-2.59025899]] 

학습 후 예측값: 
 [[0.07 ]
 [0.965]
 [0.965]
 [1.   ]] 
'''

Iris

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt


df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)


df.shape
'''
(150, 5)
'''


# 50 setosa, 50 versicolor 데이터만 사용하여 이진 분류(Binary Classification)

y = df.iloc[0:100, 4].values
y
'''
array(['Iris-setosa', 'Iris-setosa', 'Iris-setosa', 'Iris-setosa',
       'Iris-setosa', 'Iris-setosa', 'Iris-setosa', 'Iris-setosa',
       'Iris-setosa', 'Iris-setosa', 'Iris-setosa', 'Iris-setosa',
       'Iris-setosa', 'Iris-setosa', 'Iris-setosa', 'Iris-setosa',
       'Iris-setosa', 'Iris-setosa', 'Iris-setosa', 'Iris-setosa',
       'Iris-setosa', 'Iris-setosa', 'Iris-setosa', 'Iris-setosa',
       'Iris-setosa', 'Iris-setosa', 'Iris-setosa', 'Iris-setosa',
       'Iris-setosa', 'Iris-setosa', 'Iris-setosa', 'Iris-setosa',
       'Iris-setosa', 'Iris-setosa', 'Iris-setosa', 'Iris-setosa',
       'Iris-setosa', 'Iris-setosa', 'Iris-setosa', 'Iris-setosa',
       'Iris-setosa', 'Iris-setosa', 'Iris-setosa', 'Iris-setosa',
       'Iris-setosa', 'Iris-setosa', 'Iris-setosa', 'Iris-setosa',
       'Iris-setosa', 'Iris-setosa', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor',
       'Iris-versicolor', 'Iris-versicolor', 'Iris-versicolor'],
      dtype=object)
'''


# 타겟 레이블을 setosa = -1, versicolor = 1 로 변경

y = np.where(y == 'Iris-setosa', -1, 1)
y
'''
array([-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
       -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
       -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,  1,
        1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,
        1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,
        1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1])
'''


# 두 개의 특성(sepal length, petal length)만 사용
X = df.iloc[0:100, [0, 2]].values
X.shape
'''
(100, 2)
'''


# 두 특성에 따라 데이터 시각화
plt.scatter(X[:50, 0], X[:50, 1], color='red', marker='o', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1], color='blue', marker='x', label='versicolor')
plt.xlabel('sepal length')
plt.ylabel('petal length')
plt.legend(loc='upper left')
plt.show()

# 퍼셉트론 구현
class Perceptron:
    # niter = iteration 의 횟수
    def __init__(self, rate = 0.01, niter = 10):
        self.rate = rate
        self.niter = niter
        
    def fit(self, X, y):
        """
        퍼셉트론을 학습시키는 코드
        
        X : 학습되는 데이터에 해당하는 벡터
        X.shape -> [샘플의 수, 특성의 수]
        
        y : 타겟값
        y.shape -> [샘플의 수]
        """

        # 초기 가중치는 [0, 0, 0] 으로 설정
        self.weight = np.zeros(1 + X.shape[1])

        # 오분류(mis-classification)된 데이터의 수
        self.errors = [] 

        for i in range(self.niter):
            err = 0
            for xi, target in zip(X, y):
                delta_w = self.rate * (target - self.predict(xi))
                self.weight[1:] += delta_w * xi
                self.weight[0] += delta_w
                err += int(delta_w != 0.0)
            self.errors.append(err)
        return self

    def net_input(self, X):
        """
        입력값을 받아 가중치, 편향과 연산
        """
        return np.dot(X, self.weight[1:]) + self.weight[0]

    def predict(self, X):
        """
        학습 후 가중치를 바탕으로 데이터의 클래스를 예측
        """
        return np.where(self.net_input(X) >= 0.0, 1, -1)


# 퍼셉트론에 데이터를 넣어 가중치를 학습
# 학습률(learning rate): 0.1, iteration(epoch): 10
# 퍼셉트론을 학습시키고 오분류(mis-classification)의 변화를 확인
pn = Perceptron(0.1, 10)
pn.fit(X, y)
plt.plot(range(1, len(pn.errors) + 1), pn.errors, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of misclassifications')
plt.show()

# 데이터가 잘 분류 되었는지 확인
# 퍼셉트론의 결정 경계를 확인
from matplotlib.colors import ListedColormap

def plot_decision_regions(X, y, classifier, resolution=0.02):

    # 그래프 요소를 세팅
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

    # 결정 경계면
    x1_min, x1_max = X[:,  0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
    np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    # 데이터 시각화
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
        alpha=0.8, color=cmap(idx),
        marker=markers[idx], label=cl)


plot_decision_regions(X, y, classifier=pn)
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()

References

동영상

웹페이지

서적

밑바닥부터 시작하는 딥러닝

Review

input layer(입력층): 노드의 개수는 입력값에 따라서 자동으로 정해진다.
hidden layer(은닉층): 노드의 개수를 조절할 수 있다.
output layer(출력층): 신경망 모델에서 출력값을 의미하며, 이 출력층의 노드 개수, 모양에 따라서 모델의 정의가 달라질 수 있다.

Input Layer: A
Hidden Layer: B
Output Layer: D
Neuron(Node): C
Weight: F
Bias: E
Activation Function: G
Node Map: H
Iteration: I
Epoch: J

model = tf.keras.models.Sequential([
        tf.keras.layers.Flatten(input_shape=(28, 28)), 
        tf.keras.layers.Dense(256, activation='relu'),
        tf.keras.layers.Dense(10, activation='softmax') 
])

Node Map: 784 x 256 x 10

model = tf.keras.models.Sequential([
        tf.keras.layers.Flatten(input_shape=(28, 28))
])
print(model(x_train).shape)

위 코드를 실행하게 되면, (60000, 784) 형태로 출력
만일, 100장의 이미지가 이 모델에 입력된다면 출력된 array는 어떤 형태로 구성되어 있을까?
- (100, 784)
TensorFlow에서는 데이터의 개수를 주로 array의 가장 첫 번째 차원에서 다룬다.

model = tf.keras.models.Sequential([
        tf.keras.layers.Flatten(input_shape=(28, 28)), 
        tf.keras.layers.Dense(256, activation='relu'), # ----- (a)
        tf.keras.layers.Dense(10, activation='softmax') 
])

한 번에 100장의 이미지가 모델을 통과한다고 할 때, (a)에서의 입력 값과 출력 값의 array는 각각 어떤 형태로 구성되어 있을까?
- 입력: (100, 784), 출력: (100, 256)

Advanced

강의 자료 작성

Perceptron이란, 무언가를 인지하는 능력을 뜻하는 Perception과 감각 입력 정보를 의미 있는 정보로 바꿔주는 뇌의 신경세포를 뜻하는 Neuron이 합하여 만들어진 단어입니다. 뉴런이 감각 정보를 받아서 문제를 해결하는 원리를 따라 한 인공 뉴런으로써, 입력값에 대해 가중치를 적용해 계산한 후, 결과를 전달합니다. 하나의 뉴런으로 이루어진 신경망의 기본 구조이며 다수의 입력값을 받아 하나의 출력값을 내보낸다는 특징이 있습니다. 뉴런은 입력값에 가중치와 편향을 곱해진 값을 모두 더하는 연산을 하고 활성화 함수를 적용한 후 그 값을 출력합니다. 활성화 함수는 뒤 슬라이드에서 알아보겠습니다. 학습을 지속하며 손실 값이 최소가 되는 적절한 가중치를 찾는 것이 DL Model에서 중요하다고 할 수 있습니다. 편향이란 해당 Perceptron이 얼마나 쉽게 활성화되는 지를 조절하는 매개변수입니다.

Neural Network에서 각 층에 대해 알아보겠습니다. Input, Hidden, Output으로 구성되어 있으며, Input Layer는 데이터가 입력되는 층으로 입력되는 데이터셋의 특성에 따라 입력층 노드의 수가 결정됩니다. 보통 입력층은 어떤 계산도 수행하지 않고 그저 값만 전달합니다. Hidden Layer는 입력층으로 부터 입력된 신호가 가중치, 편향과 연산되는 층입니다. 은닉층에서는 입력 데이터셋의 특성 수와 상관없이 노드를 구성할 수 있으며 일반적으로 Deep Learning은 2개 이상의 은닉층을 가졌습니다. 가장 마지막에 위치한 층이 Output Layer이며 문제 종류에 따라 출력층을 잘 설계하는 것이 중요한데, 보통 이진 분류 문제에서는 Sigmoid func을 사용하며 출력층 노드 수는 1로 설정하고, 다중 분류 문제에서는 Softmax func을 사용하며 출력층의 노드 수는 Label Class 수와 동일하게 설정합니다. 회귀 문제에서는 활성화 함수를 지정해주지 않으며 노드 수는 출력값의 특성 수와 동일하게 설정합니다.

어떤 활성화 함수를 사용하느냐예 따라 출력 값이 다양해지기 때문에 적절한 함수를 사용하는 것이 중요한데, 활성화 함수란, 어떠한 신호를 입력 받아 이를 적절한 처리를 하여 출력해주는 함수입니다. 인공 신경망에서 활성화 함수는 다음 층으로 신호를 얼만큼 전달할 지 결정하는데, 간단한 세가지 함수에 대해 알아보겠습니다. 먼저 Step function은 입력 값이 임계값을 넘기면 1을 출력하고 그렇지 않으면 0을 출력하는 함수입니다. 그런데 신경망이 경사 하강법을 이용해서 학습을 진행하기 위해서는 ‘미분’과정이 필요합니다. 그 과정을 Sigmoid 함수가 해결해줍니다. 다음 ReLu 함수는 가장 많이 사용되는 활성화 함수로써 Sigmoid와 tanh가 갖는 Gradient Vanishing 문제를 해결하기 위한 함수입니다. 학습이 빠르고, 연산 비용이 적고, 구현이 매우 간단하다는 특징이 있습니다.

Machine Learning Model과의 비교

Classifier

DL

from sklearn.metrics import f1_score, accuracy_score, plot_confusion_matrix, classification_report, roc_curve, roc_auc_score
from sklearn.metrics import classification_report
from catboost import CatBoostClassifier
import tensorflow as tf
import pandas as pd
import numpy as np


df = pd.read_excel("https://ds-lecture-data.s3.ap-northeast-2.amazonaws.com/MouseProtein/mouse_protein_X.xls", header=None)
df_label = pd.read_excel("https://ds-lecture-data.s3.ap-northeast-2.amazonaws.com/MouseProtein/mouse_protein_label.xls", header=None)


print(df.isnull().sum().sum())
print(df_label.isnull().sum().sum())
'''
0
0
'''


X = df.values
y = np.where(df_label.values == 2, 0, 1) # 타겟 레이블 비정상 = 0, 정상 = 1 변경
X, y
'''
(array([[0.50364, 0.74719, 0.43018, ..., 0.83156, 0.18885, 1.6757 ],
        [0.51462, 0.68906, 0.41177, ..., 0.84927, 0.2004 , 1.7436 ],
        [0.50918, 0.73025, 0.41831, ..., 0.84671, 0.19368, 1.9264 ],
        ...,
        [0.2287 , 0.39518, 0.23412, ..., 0.97661, 0.29084, 1.4308 ],
        [0.22124, 0.41289, 0.24397, ..., 0.98929, 0.3067 , 1.404  ],
        [0.30263, 0.46106, 0.25656, ..., 1.0204 , 0.29233, 1.371  ]]),
 array([[1],
        [1],
        [1],
        ...,
        [0],
        [0],
        [0]]))
'''


model = tf.keras.models.Sequential([
        tf.keras.layers.Dense(66, activation='relu'),
        tf.keras.layers.Dense(1, activation='sigmoid')
])

model.compile(optimizer='adam',
              loss='binary_crossentropy',
              metrics=['accuracy'])

model.fit(X, y, epochs=6)
'''
Epoch 1/6
34/34 [==============================] - 1s 3ms/step - loss: 0.6811 - accuracy: 0.5525
Epoch 2/6
34/34 [==============================] - 0s 4ms/step - loss: 0.6323 - accuracy: 0.6592
Epoch 3/6
34/34 [==============================] - 0s 5ms/step - loss: 0.6114 - accuracy: 0.6713
Epoch 4/6
34/34 [==============================] - 0s 3ms/step - loss: 0.5979 - accuracy: 0.6797
Epoch 5/6
34/34 [==============================] - 0s 3ms/step - loss: 0.5843 - accuracy: 0.6908
Epoch 6/6
34/34 [==============================] - 0s 4ms/step - loss: 0.5696 - accuracy: 0.7214
<keras.callbacks.History at 0x7fe7e1d575d0>
'''


y_pred = model.predict(X) > 0.5
print(classification_report(y, y_pred))
'''
              precision    recall  f1-score   support

           0       0.68      0.84      0.75       507
           1       0.82      0.66      0.73       570

    accuracy                           0.74      1077
   macro avg       0.75      0.75      0.74      1077
weighted avg       0.76      0.74      0.74      1077

'''

ML

CatBoostClassifier

model = CatBoostClassifier()
model.fit(X, y)
'''
Learning rate set to 0.010634
0:	learn: 0.6838687	total: 47.4ms	remaining: 47.4s
1:	learn: 0.6749666	total: 80.3ms	remaining: 40.1s
2:	learn: 0.6652649	total: 115ms	remaining: 38.2s
3:	learn: 0.6585059	total: 148ms	remaining: 36.8s
'
'
'
997:	learn: 0.0127698	total: 30.8s	remaining: 61.7ms
998:	learn: 0.0127488	total: 30.8s	remaining: 30.8ms
999:	learn: 0.0127222	total: 30.9s	remaining: 0us
<catboost.core.CatBoostClassifier at 0x7fe7e1efdc10>
'''


# roc_curve(타겟값, prob of 1)
y_pred_proba = model.predict_proba(X)[:, 1]
fpr, tpr, thresholds = roc_curve(y, y_pred_proba)

roc = pd.DataFrame({
    'FPR(Fall-out)': fpr, 
    'TPRate(Recall)': tpr, 
    'Threshold': thresholds
})

# 최적의 threshold
optimal_idx = np.argmax(tpr - fpr)
optimal_threshold = thresholds[optimal_idx]
print('idx:', optimal_idx, ', threshold:', optimal_threshold)

# threshold 설정 및 레포트
y_pred_optimal = y_pred_proba >= optimal_threshold
print(classification_report(y, y_pred_optimal))

# auc 점수
auc_score = roc_auc_score(y, y_pred_optimal)
print('auc점수 : ', auc_score)
print('최종 f1 스코어',f1_score(y, y_pred_optimal))
'''
idx: 2 , threshold: 0.8921977636471232
              precision    recall  f1-score   support

           0       1.00      1.00      1.00       507
           1       1.00      1.00      1.00       570

    accuracy                           1.00      1077
   macro avg       1.00      1.00      1.00      1077
weighted avg       1.00      1.00      1.00      1077

auc점수 :  1.0
최종 f1 스코어 1.0
'''

Regressor

DL

from sklearn.metrics import mean_squared_error, r2_score
from tensorflow.keras.datasets import boston_housing
import matplotlib.pyplot as plt 
import tensorflow as tf
import lightgbm as lgb
import pandas as pd
import numpy as np


# import
(X_train, y_train), (X_test, y_test) = boston_housing.load_data()

print(len(X_train), len(X_test))
'''
404 102
'''


# 전처리, 정규화
x_mean = X_train.mean(axis=0)
x_std = X_train.std(axis=0)
X_train -= x_mean
X_train /= x_std
X_test -= x_mean
X_test /= x_std

y_mean = y_train.mean(axis=0)
y_std = y_train.std(axis=0)
y_train -= y_mean
y_train /= y_std
y_test -= y_mean
y_test /= y_std

print(X_train[0])
print(y_train[0])
'''
[-0.27224633 -0.48361547 -0.43576161 -0.25683275 -0.1652266  -0.1764426
  0.81306188  0.1166983  -0.62624905 -0.59517003  1.14850044  0.44807713
  0.8252202 ]
-0.7821526033779157
'''


model = tf.keras.Sequential([
  tf.keras.layers.Dense(units=52, activation='relu', input_shape=(13, )), 
  tf.keras.layers.Dense(units=39, activation='relu'), 
  tf.keras.layers.Dense(units=26, activation='relu'), 
  tf.keras.layers.Dense(units=1)
])

model.compile(optimizer=tf.keras.optimizers.Adam(lr=0.07), loss='mse')
history = model.fit(X_train, y_train, epochs=25, batch_size=32, validation_split=0.25, 
                    callbacks=[tf.keras.callbacks.EarlyStopping(patience=3, monitor='val_loss')])
'''
Epoch 1/25
10/10 [==============================] - 1s 14ms/step - loss: 2.2057 - val_loss: 0.6653
Epoch 2/25
10/10 [==============================] - 0s 5ms/step - loss: 0.3589 - val_loss: 0.5064
Epoch 3/25
10/10 [==============================] - 0s 4ms/step - loss: 0.3239 - val_loss: 0.4138
Epoch 4/25
10/10 [==============================] - 0s 4ms/step - loss: 0.2633 - val_loss: 0.4229
Epoch 5/25
10/10 [==============================] - 0s 6ms/step - loss: 0.2389 - val_loss: 0.3672
Epoch 6/25
10/10 [==============================] - 0s 6ms/step - loss: 0.2340 - val_loss: 0.3800
Epoch 7/25
10/10 [==============================] - 0s 7ms/step - loss: 0.1994 - val_loss: 0.3231
Epoch 8/25
10/10 [==============================] - 0s 7ms/step - loss: 0.2063 - val_loss: 0.4477
Epoch 9/25
10/10 [==============================] - 0s 7ms/step - loss: 0.2255 - val_loss: 0.4122
Epoch 10/25
10/10 [==============================] - 0s 5ms/step - loss: 0.2743 - val_loss: 0.3224
Epoch 11/25
10/10 [==============================] - 0s 5ms/step - loss: 0.3203 - val_loss: 0.4504
Epoch 12/25
10/10 [==============================] - 0s 5ms/step - loss: 0.2567 - val_loss: 0.2192
Epoch 13/25
10/10 [==============================] - 0s 6ms/step - loss: 0.1652 - val_loss: 0.1671
Epoch 14/25
10/10 [==============================] - 0s 7ms/step - loss: 0.1365 - val_loss: 0.1489
Epoch 15/25
10/10 [==============================] - 0s 5ms/step - loss: 0.1104 - val_loss: 0.1451
Epoch 16/25
10/10 [==============================] - 0s 5ms/step - loss: 0.1041 - val_loss: 0.1376
Epoch 17/25
10/10 [==============================] - 0s 7ms/step - loss: 0.1090 - val_loss: 0.2205
Epoch 18/25
10/10 [==============================] - 0s 4ms/step - loss: 0.1150 - val_loss: 0.1587
Epoch 19/25
10/10 [==============================] - 0s 7ms/step - loss: 0.1022 - val_loss: 0.1670
Epoch 20/25
10/10 [==============================] - 0s 5ms/step - loss: 0.1116 - val_loss: 0.1511
Epoch 21/25
10/10 [==============================] - 0s 4ms/step - loss: 0.1004 - val_loss: 0.1764
Epoch 22/25
10/10 [==============================] - 0s 4ms/step - loss: 0.0925 - val_loss: 0.1686
Epoch 23/25
10/10 [==============================] - 0s 4ms/step - loss: 0.0786 - val_loss: 0.1628
Epoch 24/25
10/10 [==============================] - 0s 4ms/step - loss: 0.0930 - val_loss: 0.1347
Epoch 25/25
10/10 [==============================] - 0s 7ms/step - loss: 0.0884 - val_loss: 0.1536
'''


model.evaluate(X_test, y_test)
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print('Mean squared error: ', mse)
print('R2 score: ', r2)
'''
Mean squared error:  0.28229374909008303
R2 score:  0.7130318527838599
'''


plt.plot(history.history['loss'], 'b-', label='loss')
plt.plot(history.history['val_loss'], 'r--', label='val_loss')
plt.xlabel('Epoch')
plt.legend()
plt.show()

loss가 무조건 줄어드는 것 만은 아니다.

ML

LGBM regressoion 간단하게 구현

train_ds = lgb.Dataset(X_train, label = y_train) 
test_ds = lgb.Dataset(X_test, label = y_test)

params = {'learning_rate': 0.01, 
          'max_depth': 10,
          'objective': 'regression', 
          'metric': 'mse', 
          'is_training_metric': True, 
          'num_leaves': 144, 
          'feature_fraction': 0.9, 
          'bagging_fraction': 0.7, 
          'bagging_freq': 5, 
          'seed':2018}

model = lgb.train(params, train_ds, 1000, test_ds, verbose_eval=100, early_stopping_rounds=100)
'''
Training until validation scores don't improve for 100 rounds.
[100]	valid_0's l2: 0.327187
[200]	valid_0's l2: 0.197992
[300]	valid_0's l2: 0.163687
[400]	valid_0's l2: 0.15169
[500]	valid_0's l2: 0.146331
[600]	valid_0's l2: 0.14271
[700]	valid_0's l2: 0.139874
[800]	valid_0's l2: 0.138576
[900]	valid_0's l2: 0.137909
[1000]	valid_0's l2: 0.139408
Did not meet early stopping. Best iteration is:
[925]	valid_0's l2: 0.137139
'''


y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print('Mean squared error: ', mse)
print('R2 score: ', r2)
'''
Mean squared error:  0.1371388347018278
R2 score:  0.8605903338893786
'''

머신러닝 모델보다 딥 러닝 모델이 더 나을 것이라고 했지만, 기본과제든 도전과제든 머신러닝 모델이 더 좋은 성능을 보였다.
아마 두개의 데이터셋 모두 전처리가 크게 필요없는 데이터셋이라서 그런 것 같기도하고, 현재 존재하는 머신러닝 모델들의 성능도 뒤지지 않기 때문에 그런 것 같다. 그것도 아니라면 딥 러닝 모델링 더 배워야 할 수도?
결론: 전처리를 빡세게만 한다면 머신러닝 모델! 전처리 하기 귀찮다면 딥러닝 모델!

목차

1주차

2주차

3주차