[알고리즘] 알고리즘의 복잡도 표현 방법

Posted on | In
알고리즘 복잡도의 개념 및 필요 이유. 알고리즘 성능 표기법과 빅-오 표기법

알고리즘 복잡도

알고리즘 복잡도 계산이 필요한 이유

  • 하나의 문제를 푸는 알고리즘은 다양하다.
  • 다양한 알고리즘 중 어느 알고리즘이 좋은 지 분석하기 위해, 복잡도를 정의하고 계산한다.

알고리즘 복잡도 계산 항목

  • 시간 복잡도(중요): 알고리즘 실행 속도
  • 공간 복잡도: 알고리즘이 사용하는 메모리 사이즈

시간 복잡도의 주요 요소

  • 입력의 크기가 커지면 커질수록 반복문이 알고리즘 수행 시간을 지배한다.

알고리즘 성능 표기법

  • 빅-오(Big-O) 표기법: O(N)
    • 알고리즘 최악의 실행 시간을 표기한다.
    • 가장 많이/일반적으로 사용한다.
    • 아무리 최악의 상황이라도, 이 정도의 성능은 보장한다는 의미이기 때문이다.
  • 오메가(Ω) 표기법: Ω(N)
    • 오메가 표기법은 알고리즘 최상의 실행 시간을 표기한다.
  • 세타(Θ) 표기법: Θ(N)
    • 오메가 표기법은 알고리즘 평균 실행 시간을 표기한다.

시간 복잡도 계산은 반복문이 핵심 요소임을 인지하고, 계산 표기는 최상, 평균, 최악 중, 최악의 시간인 빅오 표기법을 중심으로 익힌다.

빅-오(Big-O) 표기법

  • O(입력)
    • 입력 $n$에 따라 결정되는 시간 복잡도 함수이다.
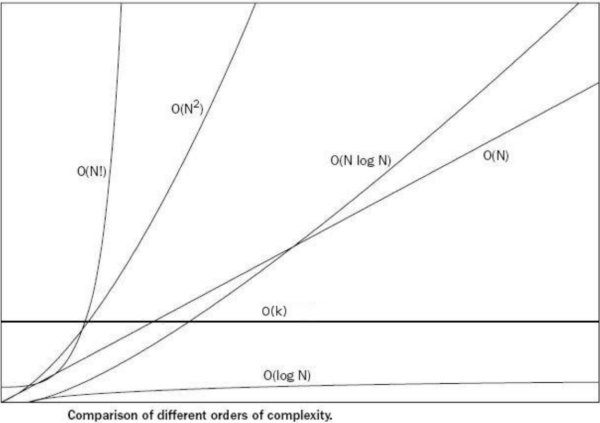
    • O(1), O($log n$), O(n), O(n$log n$), O($n^2$), O($2^n$), O(n!)등으로 표기한다.
    • 입력 $n$의 크기에 따라 기하급수적으로 시간 복잡도가 늘어날 수 있다.
      • O(1) < O($log n$) < O(n) < O(n$log n$) < O($n^2$) < O($2^n$) < O(n!)
        • 참고: $log n$의 베이스는 2 - $log_2 n$
  • 단순하게 입력 $n$에 따라, 몇 번 실행이 되는지를 계산하면 된다.
    • 표현식에 가장 큰 영향을 미치는 $n$의 단위로 표기한다.
    • $n$이 1이든 100이든, 1000이든, 10000이든,
      • 무조건 2회(상수회) 실행: O(1) 
        1
        2
              if n > 10:
           print(n)
      • $n$에 따라, $n$번, $n + 10$번, 또는 $3n + 10$번 등 실행: O($n$) 
        1
        2
        3
        4
              variable = 1
      for num in range(3):
          for index in range(n):
               print(index)
      • $n$에 따라, $n^2$번, $n^2$ + 1000 번, 100$n^2$ - 100, 또는 300$n^2$ + 1번 등 실행: O($n^2$) 
        1
        2
        3
        4
        5
              variable = 1
      for i in range(300):
          for num in range(n):
              for index in range(n):
                   print(index)

0%